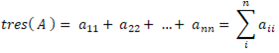ΕΙΣΑΓΩΓΗ
Η Γραμμική Άλγεβρα είναι ένας κλάδος των μαθηματικών που ασχολείται με γραμμικά συστήματα εξισώσεων και τους μετασχηματισμούς τους. Παρέχει μια ισχυρή εργαλειοθήκη για την ανάλυση και την επίλυση προβλημάτων που σχετίζονται με διανύσματα, πίνακες και γραμμικούς μετασχηματισμούς. Με το ευρύ φάσμα εφαρμογών της σε τομείς όπως τα γραφικά υπολογιστών, η μηχανική μάθηση και η φυσική, η γραμμική άλγεβρα είναι ένα ουσιαστικό μάθημα για τους μαθητές σε πολλούς τομείς. Η κατανόηση των εννοιών και των τεχνικών της γραμμικής άλγεβρας είναι κρίσιμη για την ανάπτυξη μιας βαθύτερης κατανόησης των μαθηματικών και επιστημονικών ιδεών, καθώς και για την επιτυχία σε πολλές τεχνικές σταδιοδρομίες.
Η Αναλυτική Γεωμετρία, γνωστή και ως γεωμετρία συντεταγμένων, είναι ένας κλάδος των μαθηματικών που χρησιμοποιεί αλγεβρικές μεθόδους για τη μελέτη γεωμετρικών σχημάτων και σχημάτων σε δισδιάστατους και τρισδιάστατους χώρους. Στην αναλυτική γεωμετρία, τα σημεία, οι ευθείες και οι καμπύλες αναπαρίστανται χρησιμοποιώντας μαθηματικές εξισώσεις και οι σχέσεις τους αναλύονται και μελετώνται χρησιμοποιώντας μαθηματικές τεχνικές. Αυτός ο κλάδος των μαθηματικών παρέχει ένα ισχυρό εργαλείο για την απεικόνιση και την κατανόηση γεωμετρικών αντικειμένων και την επίλυση γεωμετρικών προβλημάτων και χρησιμοποιείται ευρέως σε τομείς όπως η μηχανική, η φυσική και τα γραφικά υπολογιστών. Η κατανόηση των αρχών της αναλυτικής γεωμετρίας είναι απαραίτητη για τους μαθητές που επιθυμούν να ακολουθήσουν σταδιοδρομία σε αυτούς τους τομείς ή να μελετήσουν πιο προχωρημένα θέματα στα μαθηματικά και τις επιστήμες.
Προγραμμα υπολογισμου ασκησεων
Με το παρόν πρόγραμμα μπορείτε να υπολογίσετε :
- Γραμμικά συστήματα της μορφής Αx= b
- Ιδιοτιμές, ιδιοδιανύσματα
- Διαγωνοποίηση πίνακα Α
- Πράξεις με πίνακες όπως:
- Πρόσθεση 2 πινάκων,
- Πολλαπλασιασμό 2 πινάκων,
- Ορίζουσες,
- Αντίστροφους πίνακες
- Ίχνος πίνακα,
- Βαθμό πίνακα
- Πολλαπλασιασμός με αριθμό,
- Ύψωση πίνακα σε δύναμη
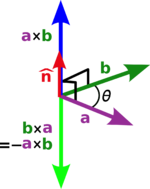
- Εσωτερικό, εξωτερικό και μικτό γινόμενο διανυσμάτων
- Γωνία δύο διανυσμάτων
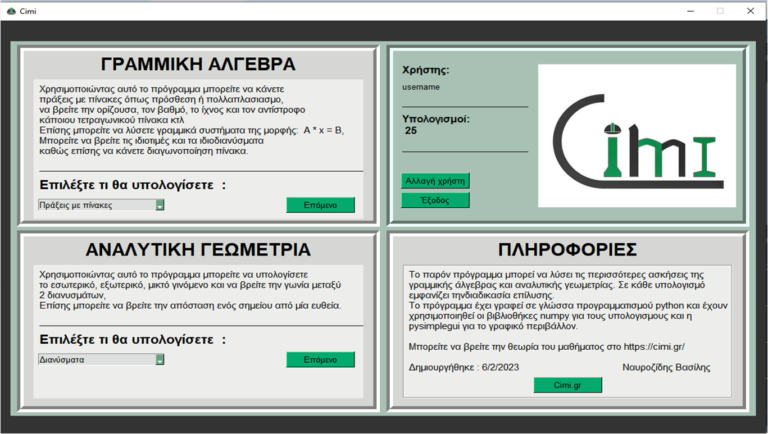
Το πρόγραμμα εμφανίζει τα αποτελέσματα μαζί με την μεθοδολογία επίλυσης βήμα προς βήμα. Το αρχικό παράθυρο του προγράμματος φαίνεται στην παρακάτω εικόνα. Μπορείτε να κατεβάσετε το πρόγραμμα Cimi πατώντας το κουμπί download στα δεξιά
Διαδικασία εγκατάστασης μόνο για windows:
- Κατεβάζετε το αρχείο Cimi_01.zip πατώντας το κουμπί DOWNOLAD
- Αποσυμπιέζετε το αρχείο Cimi_01.zip μόλις ολοκληρωθεί η λήψη
- διπλό κλικ στο Cimi_01.exe για εκτέλεση
* Χώρος αποθήκευσης 39 mb *
Επίσης μπορείτε να δημιουργήσετε μια συντόμευση του Cimi.exe στην επιφάνεια εργασίας για πιο γρήγορη πρόσβαση.
ΛΟΓΙΣΜΟΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ
Επίσης μπορείτε να κατεβάσετε το integral_calculator για υπολογισμό οποιουδήποτε ολοκληρώματος.
Πίνακες
ΤΙ ΕΙΝΑΙ Ο ΠΙΝΑΚΑΣ
Πίνακας είναι η διάταξη αριθμών, συμβόλων, ή εκφράσεων σε γραμμές και στήλες. Τα μεμονωμένα στοιχεία σε ένα πίνακα ονομάζονται στοιχεία ή εγγραφές του. Χρησιμοποιούνται σε πάρα πολλούς τομείς των μαθηματικών όπως η γραμμική άλγεβρα, οι πιθανότητες, η στατιστική καθώς και σε άλλες επιστήμες όπως η μηχανική, ηλεκτρικά κυκλώματα, πληροφορική, οικονομικά, κ.α.
Παράδειγμα : Μια αλυσίδα σούπερ μάρκετ έχει τρία (Α, Β, Γ) καταστήματα σε δύο πόλεις (ΑΘΗΝΑ, ΞΑΝΘΗ) . Ο πίνακας περιέχει τις ποσότητες ενός προϊόντος στα καταστήματα αυτά:
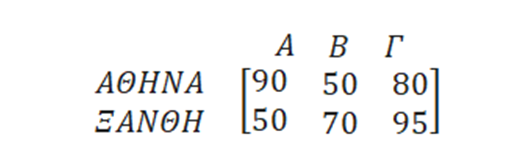
Ο πίνακας έχει διάσταση 3×2 δηλαδή τρείς γραμμές και δύο στήλες.
ΕΙΔΗ ΠΙΝΑΚΩΝ
Ανάλογα με την διάσταση του ο πίνακας χωρίζεται σε τετραγωνικό πίνακα, πίνακα στήλη, πίνακα γραμμή, πίνακα στοιχείο και μηδενικός πίνακας,
- Tετραγωνικός πίνακας είναι ο πίνακας του οποίου ο αριθμός των γραμμών (n) είναι ίσος με τον αριθμό των στηλών (m) δηλαδή όταν n=m ( n x m).
- Πίνακας στήλη είναι ο πίνακας του οποίου ο αριθμός των στηλών (m) είναι 1 και ο αριθμός των γραμμών n ( n x 1).
- Πίνακας γραμμή είναι ο πίνακας του οποίου ο αριθμός των γραμμών (n) είναι 1 και ο αριθμός των στηλών m ( 1 x m).
- Πίνακας στοιχείο είναι ο πίνακας του οποίου ο αριθμός των γραμμών (n) είναι 1 και ο αριθμός των στηλών m είναι 1 δηλαδή ( 1 x 1). Ο πίνακας στοιχείο είναι τετραγωνικός πίνακας.
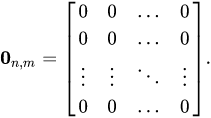
- Μηδενικός πίνακας είναι ο πίνακας (n x m) του οποίου όλα τα στοιχεία είναι ίσα με μηδέν.
- Ανάστροφος πίνακας του Α (ο οποίος συμβολίζεται με Α™ ή Α’) είναι ο πίνακας που προκύπτει από τον Α αν κάνουμε τις γραμμές του στήλες και τις στήλες του γραμμές.
Δηλαδή, Αij=A’ji και αν ο Α είναι διαστάσεων n x m τότε ο Α’ είναι διαστάσεων m x n .
Κύρια διαγώνιος (Δ) ενός τετραγωνικού πίνακα n x n είναι τα n στοιχεία του α11, α22, …, αnn. Δ = ( α11, α22, …, αnn ).
Ιχνος του Α ( tres(A) ) καλείται το άθροισμά των στοιχείων της κύριας διαγωνίου.
- Διαγώνιος τετραγωνικός πίνακας είναι ο πίνακας n x n του οποίου όλα τα στοιχεία είναι μηδέν εκτός από τα στοιχεία της διαγωνίου του.
- Τριγωνικός άνω είναι ένας πίνακας n x n του οποίου όλα τα στοιχεία κάτω από την διαγώνιο είναι μηδέν.
- Τριγωνικός κάτω είναι ένας πίνακας n x n του οποίου όλα τα στοιχεία πάνω από την διαγώνιο είναι μηδέν.
Δηλαδή ένας τετραγωνικός πίνακας Α είναι άνω (αντίστοιχα κάτω) τριγωνικός όταν όλα τα στοιχεία του που είναι κάτω (αντίστοιχα πάνω) από την κύρια διαγώνιο είναι μηδέν.
- Συμμετρικός πίνακας είναι ένας τετραγωνικός πίνακα Α n x n αν ταυτίζεται με τον ανάστροφό του Α’. Δηλαδή Α = Α’
- Αντισυμμετρικός πίνακας είναι ένας τετραγωνικός πίνακα Α n x n αν είναι αντίθετος με τον ανάστροφό του Α’ . Δηλαδή Α = – Α’
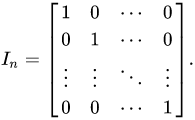
- Μοναδιαίος πίνακας, Iν είναι ο διαγώνιος πίνακας του οποίου όλα τα στοιχεία της κύριας διαγωνίου είναι μονάδα και τα υπόλοιπα μηδέν
Μπορείτε να κατεβάσετε το integral_calculator για υπολογισμό οποιουδήποτε ολοκληρώματος.
ΠΡΑΞΕΙΣ ΠΙΝΑΚΩΝ
- Άθροισμα των πινάκων n x m Α, Β ορίζουμε τον n x m πίνακα Γ, όπου Γ = Α + Β. Τα στοιχεία του οποίου είναι το άθροισμα των αντίστοιχων στοιχείων των Α και Β.
- Διαφορά των πινάκων n x m Α, Β ορίζουμε τον n x m πίνακα Γ, όπου Γ = Α – Β. Τα στοιχεία του οποίου είναι η διαφορά των αντίστοιχων στοιχείων των Α και Β.
Για την πρόσθεση πινάκων ισχύει η αντιμεταθετική και προσεταιριστική ιδιότητα καθώς και το ότι ο αντίστοιχος μηδενικός πίνακας αποτελεί το ουδέτερο στοιχείο της. Δηλαδή για οποιουσδήποτε n x m πίνακες Α, Β, Γ ισχύει:
- Α + Β = Β +Α
- Α + 0 = Α
- (Α +Β ) + Γ = Α + ( Β + Γ )
- Μια ακόμη πράξη είναι ο πολλαπλασιασμός αριθμού (λ) με πίνακα Α. Δηλαδή, προκύπτει ο πίνακας λΑ αν πολλαπλασιάσουμε όλα τα στοιχεία του Α επί λ. Μπορείτε να κάνετε αυτή την πράξη στο ypologismos.gr. Ιδιότητες:
- λ(Α+Β)=λΑ+λΒ
- λ(μΑ)=(λμ)Α
- (λ+μ)Α=λΑ+μΑ
- A=A και (-1)A=-A
- Γινόμενο πινάκων AB δύο πινάκων Α και Β: (περισσότερα εδώ)
- Ορίζεται πάντα για τετραγωνικούς πίνακες.
- Δεν ορίζεται για οπουσδήποτε πίνακες Α και Β. Ορίζεται μόνο αν ο αριθμός στηλών του πρώτου πίνακα (Α) είναι ίσος με τον αριθμό γραμμών του δεύτερου (Β).
- Δεν είναι αντιμεταθετική πράξη, δηλαδή ισχύει: ΑΒ ≠ ΒΑ
Στις παρακάτω δύο φωτογραφίες φαίνεται ο υπολογισμός προσθεσης και γινομένου δύο πινάκων απο το πρόγραμμα υπολογισμού Cimi.
ΠΡΟΣΘΕΣΗ ΠΙΝΑΚΩΝ
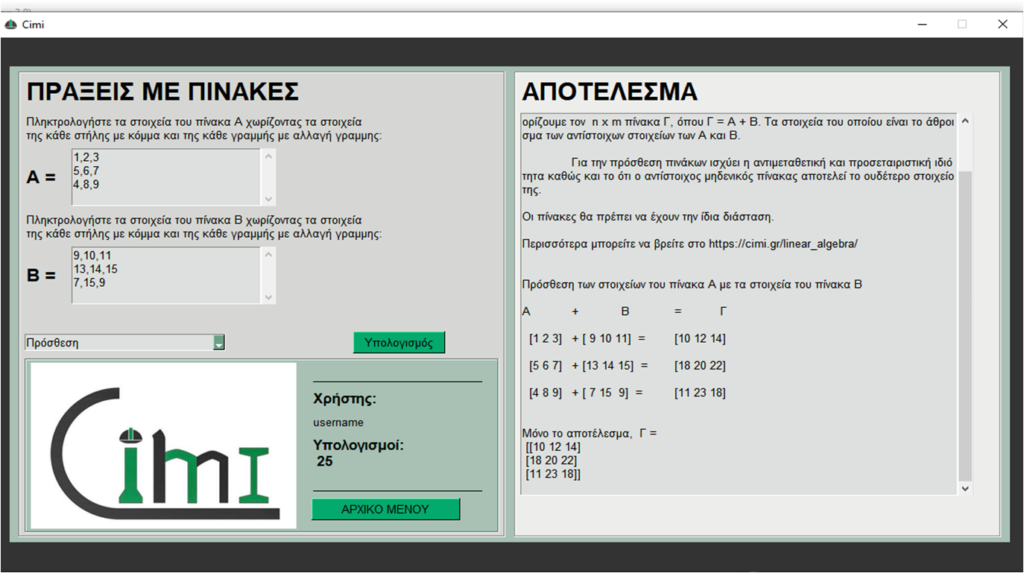
ΓΙΝΟΜΕΝΟ ΠΙΝΑΚΩΝ
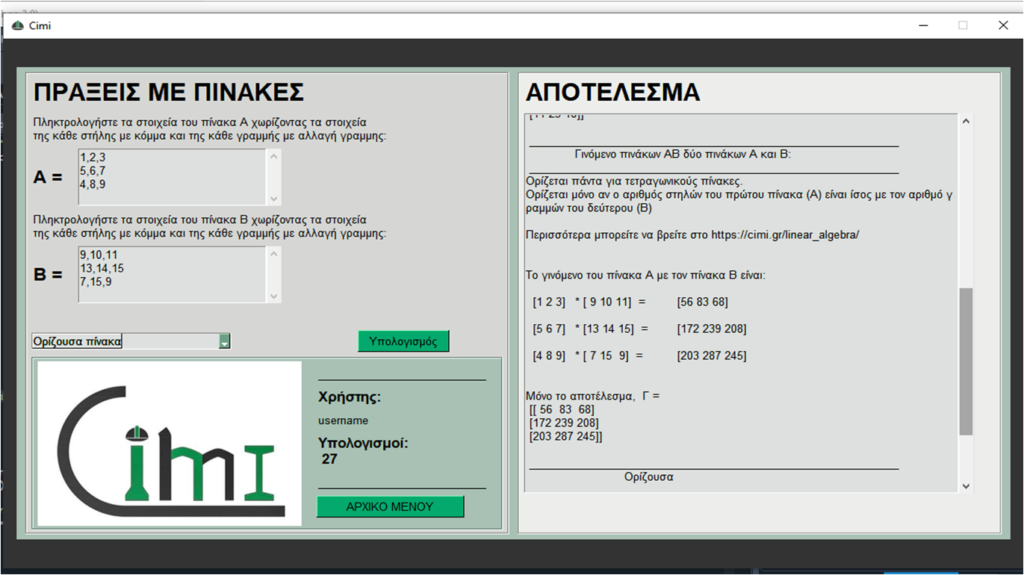
ΟΡΙΖΟΥΣΕΣ
Ως ορίζουσα ενός τετραγωνικού πίνακα Α ορίζουμε ⌈Α⌉ ή det (A):
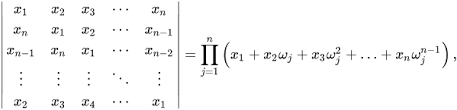
Η ορίζουσα ενός τριγωνικού πίνακα είναι ίση με το γινόμενο των στοιχείων της κύριας διαγωνίου της.
Ιδιότητες
- Αν όλα τα στοιχεία μιας στήλης ή γραμμής ενός τετραγωνικού πίνακα είναι μηδέν τότε η ορίζουσα του είναι μηδέν.
- Αν όλα τα στοιχεία μιας στήλης ή γραμμής ένος πίνακα Α πολλαπλασιαστούν με έναν αριθμό λ τότε και η ορίζουσα ⌈Α⌉ πολλαπλασιάζεται με λ.
- Αν δύο στήλες ή γραμμές μιας ορίζουσας είναι ίδιες, τότε η ορίζουσα είναι ίση με μηδέν.
- Αν ανταλλάξουμε δύο στήλες ή γραμμές ενός πίνακα τότε η ορίζουσα του πολλαπλασιάζεται επι – 1.
- Η τιμή μιας ορίζουσας δεν αλλάζει αν προσθέσουμε σε μια στήλη/γραμμή της το γινόμενο μιας άλλης στήλης/γραμμής της επί έναν οποιοδήποτε πραγματικό αριθμό.
- Η ορίζουσα κάθε τετραγωνικού πίνακα είναι ίση με την ορίζουσα του ανάστροφου πίνακα.
ΑΝΤΙΣΤΡΟΦΟΣ ΠΙΝΑΚΑΣ
Στη γραμμική άλγεβρα, ένας πίνακας Α λέγεται ότι έχει αντίστροφο εάν υπάρχει ένας άλλος πίνακας Α^(-1), που ονομάζεται αντίστροφος πίνακας, έτσι ώστε όταν οι δύο πίνακες πολλαπλασιάζονται, το αποτέλεσμα να είναι ο πίνακας ταυτότητας Ι (μοναδιαίος πίνακας). Ο αντίστροφος πίνακας, που συμβολίζεται με A^-1, ικανοποιεί την εξίσωση:
A * A^(-1) = A^(-1) * A = I
όπου I είναι ο πίνακας ταυτότητας.
Ο αντίστροφος πίνακας είναι μια αναπαράσταση του αντίστροφου πίνακα και εμφανίζει τα στοιχεία του A^-1 σε μορφή πίνακα. Αυτό μπορεί να είναι χρήσιμο για την επαλήθευση της ορθότητας ενός υπολογιζόμενου αντίστροφου πίνακα, καθώς και για την επίλυση συστημάτων γραμμικών εξισώσεων χρησιμοποιώντας μεθόδους πινάκων.
Είναι σημαντικό να σημειωθεί ότι δεν έχουν όλοι οι πίνακες αντίστροφους. Ένας πίνακας έχει αντίστροφο μόνο αν είναι τετραγωνικός και αν η ορίζουσά του δεν είναι μηδενική.
Συνοπτικά, ο αντίστροφος πίνακας είναι μια οπτική αναπαράσταση του αντίστροφου ενός πίνακα και μπορεί να χρησιμοποιηθεί για την επίλυση συστημάτων γραμμικών εξισώσεων χρησιμοποιώντας μεθόδους πινάκων.
Μπορείτε να κατεβάσετε το integral_calculator για υπολογισμό οποιουδήποτε ολοκληρώματος.
οριζουσα και αντιστροφοσ πινακα
Στην παρακάτω εικόνα φαίνεται ο υπολογισμός της ορίζουσας και του αντίστροφου πίνακα Α με το προγραμμα υπολογισμου Cimi. Ο χρήστης έχει πληκτρολογήσει τα στοιχεία του Α, έχει επιλέξει τι θα υπολογίσει από το menu και πατώντας το κουμπί Υπολογισμός εμφανίεται στο δεξιό παράθυρο (ΑΠΟΤΕΛΕΣΜΑΤΑ) ο αντίστροφος πίνακας του Α.
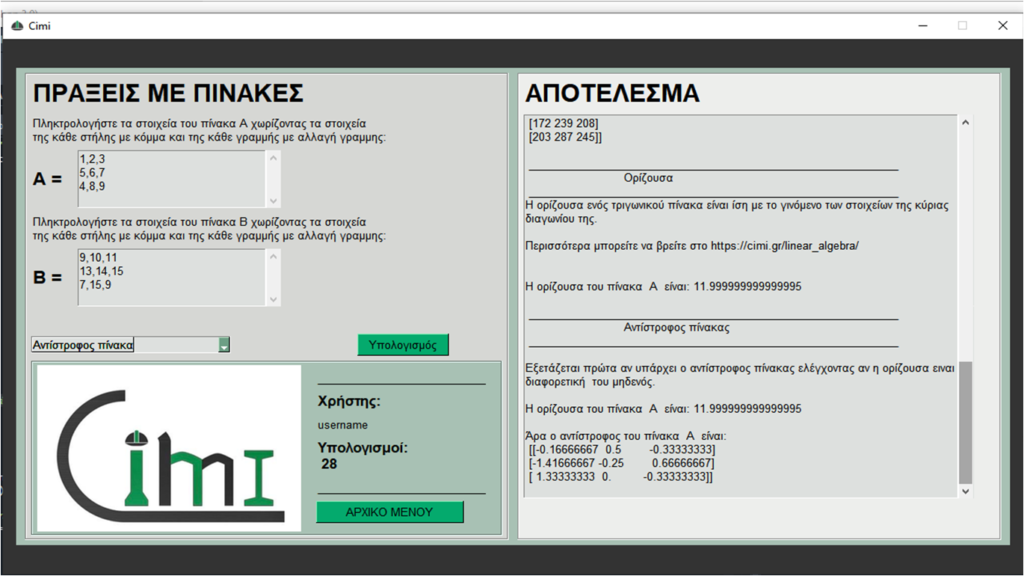
ΒΑΘΜΟΣ ΠΙΝΑΚΑ
Στη γραμμική άλγεβρα, ο βαθμός ενός πίνακα Α ορίζεται ως ο μέγιστος αριθμός γραμμικά ανεξάρτητων στηλών (ή γραμμών) στον πίνακα, δηλαδή τη μέγιστη διάσταση ενός τετραγωνικού υποπίνακα του με μη μηδενική ορίζουσα.
Σημείωση:
- Αν όλες οι υποορίζουσες του Α είναι μηδέν χωρίς ο Α να είναι ο μηδενικός πίνακας, τότε ο βαθμός του ορίζεται να είναι 1.
- Αν η ορίζουσα ενός nxn τετραγωνικού πίνακα Α είναι μη μηδενική, τότε ο βαθμός του είναι n
Ο βαθμός ενός πίνακα είναι μια κρίσιμη έννοια στη γραμμική άλγεβρα και έχει αρκετές σημαντικές εφαρμογές. Μπορεί να χρησιμοποιηθεί για τον προσδιορισμό του χώρου λύσης ενός συστήματος γραμμικών εξισώσεων, για τον υπολογισμό της ορίζουσας ενός πίνακα και για τη μελέτη των ιδιοτήτων των γραμμικών μετασχηματισμών.
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
ΤΙ ΕΙΝΑΙ ΕΝΑ ΓΡΑΜΜΙΚΟ ΣΥΣΤΗΜΑ
Ένα γραμμικό σύστημα είναι ένα σύνολο γραμμικών εξισώσεων που αντιπροσωπεύουν μια σχέση μεταξύ μεταβλητών. Στη γραμμική άλγεβρα, τα γραμμικά συστήματα μελετώνται για την κατανόηση των σχέσεων μεταξύ των μεταβλητών και για την εύρεση των λύσεών τους.
Μια γραμμική εξίσωση είναι μια εξίσωση της μορφής ax + b = 0, όπου x είναι η μεταβλητή και a, b είναι συντελεστές. Σε ένα γραμμικό σύστημα, πολλαπλές γραμμικές εξισώσεις συνδυάζονται για να αναπαραστήσουν τις σχέσεις μεταξύ πολλαπλών μεταβλητών. Για παράδειγμα, ένα γραμμικό σύστημα δύο εξισώσεων και δύο μεταβλητών μπορεί να μοιάζει με αυτό:
ax + by = c
dx + ey = f
Όπου x και y είναι οι μεταβλητές και a, b, c, d, e και f είναι συντελεστές.
Ο στόχος στην επίλυση ενός γραμμικού συστήματος είναι να βρεθούν οι τιμές των μεταβλητών (δηλαδή τα x, y για το παραπάνω παράδειγμα) που ικανοποιούν όλες τις εξισώσεις του συστήματος.
Τα γραμμικά συστήματα έχουν ένα ευρύ φάσμα εφαρμογών, από τη μοντελοποίηση πραγματικών προβλημάτων σε τομείς όπως η οικονομία και η φυσική, έως την επίλυση προβλημάτων στα γραφικά υπολογιστών και τη μηχανική μάθηση. Η κατανόηση των γραμμικών συστημάτων και ο τρόπος επίλυσής τους είναι σημαντικό μέρος της γραμμικής άλγεβρας και έχει εκτεταμένες επιπτώσεις σε πολλούς άλλους τομείς των μαθηματικών και της επιστήμης.
Συνοπτικά, ένα γραμμικό σύστημα είναι ένα σύνολο γραμμικών εξισώσεων που αντιπροσωπεύουν σχέσεις μεταξύ μεταβλητών. Ο στόχος στην επίλυση ενός γραμμικού συστήματος είναι να βρεθούν οι τιμές των μεταβλητών που ικανοποιούν όλες τις εξισώσεις του συστήματος, και αυτό μπορεί να γίνει χρησιμοποιώντας διάφορες μεθόδους. Τα γραμμικά συστήματα έχουν σημαντικές εφαρμογές σε πολλά πεδία και αποτελούν κρίσιμο μέρος της γραμμικής άλγεβρας.
Μπορείτε να κατεβάσετε το integral_calculator για υπολογισμό οποιουδήποτε ολοκληρώματος.
ΤΡΟΠΟΙ ΕΠΙΛΥΣΗΣ ΓΡΑΜΜΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
Υπάρχουν διάφορες μέθοδοι για τον υπολογισμό ενός γραμμικού συστήματος, όπως:
- Μέθοδος αντικατάστασης: Σε αυτή τη μέθοδο, μια από τις εξισώσεις επιλύεται για μια μεταβλητή και η έκφραση που προκύπτει αντικαθίσταται στην άλλη εξίσωση. Αυτό δημιουργεί μια νέα εξίσωση σε μία μεταβλητή, η οποία μπορεί να λυθεί για την τιμή αυτής της μεταβλητής. Η τιμή της δεύτερης μεταβλητής μπορεί στη συνέχεια να βρεθεί αντικαθιστώντας τις τιμές των μεταβλητών ξανά σε οποιαδήποτε από τις αρχικές εξισώσεις.
- Μέθοδος εξάλειψης: Σε αυτή τη μέθοδο, οι συντελεστές μιας από τις μεταβλητές πολλαπλασιάζονται ή διαιρούνται σε μία από τις εξισώσεις έτσι ώστε όταν οι δύο εξισώσεις προστίθενται ή αφαιρούνται, μία από τις μεταβλητές εξαλείφεται. Η προκύπτουσα εξίσωση μπορεί στη συνέχεια να λυθεί για την τιμή της υπόλοιπης μεταβλητής και η τιμή της εξαλειφθείσας μεταβλητής μπορεί να βρεθεί αντικαθιστώντας τις τιμές των μεταβλητών ξανά σε οποιαδήποτε από τις αρχικές εξισώσεις.
- Μέθοδος μητρώων (πινάκων) : Σε αυτή τη μέθοδο το σύστημα έχει την μορφή Αx=b όπου:
- Α: είναι ένας πίνακας με τους συντελεστές των μεταβλητών
- b: είναι ένας πίνακας με τους σταθερούς όρους και
- x είναι ένας πίνακας με τις μεταβλητές
Για να λυθεί ένα σύστημα πρέπι να υπάρχει αντίστροφος του Α έτσι ώστε το σύστημα να πάρει την μορφή x = b A^(-1) και να λυθεί ως προς x.
Είναι σημαντικό να σημειωθεί ότι ορισμένα γραμμικά συστήματα μπορεί να μην έχουν λύση, ενώ άλλα μπορεί να έχουν άπειρο αριθμό λύσεων. Αυτό θα εξαρτηθεί από την ορίζουσα του πίνακα Α.
Συνοπτικά, υπάρχουν πολλές μέθοδοι για τον υπολογισμό ενός γραμμικού συστήματος, συμπεριλαμβανομένης της μεθόδου αντικατάστασης, της μεθόδου εξάλειψης και της μεθόδου μήτρας. Η επιλογή της μεθόδου θα εξαρτηθεί από το συγκεκριμένο σύστημα και τις προτιμήσεις του ατόμου που επιλύει το σύστημα. Η κατανόηση αυτών των μεθόδων και το πότε πρέπει να χρησιμοποιηθούν είναι ένα σημαντικό μέρος της γραμμικής άλγεβρας
παραδειγματα
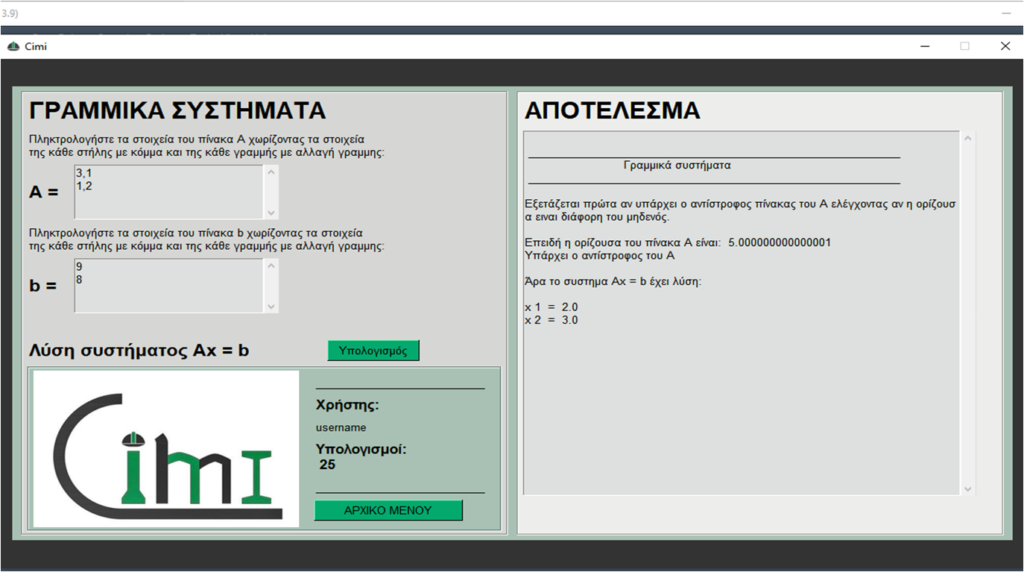
Πρέπει να λυθεί το παρακάτω σύστημα ( της μορφής Αx=b) :
3x + 1y = 9
1x + 2y = 8
Τα στοιχεία του πίνακα Α είναι οι συντελεστές των μεταβλητών x, y δηλαδή οι αριθμοί 3, 1, 1, 2. Πληκτρολογούνται τα στοιχεία του Α στο πρόγραμμα υπολογισμού Cimi όπως φαινεται στην παρακάτω εικόνα.
Τα στοιχεία του πίνακα b είναι οι σταθερόι όροι των εξισώσεων δηλαδή το 9, 8. Αντίστοιχα πληκτρολογούνται τα στοιχεια του πίνακα b στο πρόγραμμα υπολογισμού Cimi όπως φαινεται στην παρακάτω εικόνα.
Ο χρήστης πατώντας το κουμπί Υπολογισμός εμφανίζεται στο δεξιό παράθυρο (ΑΠΟΤΕΛΕΣΜΑΤΑ) ο πίνακας με τις μεταβλητές x
διανυσματα
ΤΙ ΕΙΝΑΙ ΤΑ ΔΙΑΝΥΣΜΑΤΑ
Τα διανύσματα είναι μια θεμελιώδης έννοια στη γραμμική άλγεβρα και στα μαθηματικά ευρύτερα. Ένα διάνυσμα είναι ένα μαθηματικό αντικείμενο που έχει και μέγεθος και κατεύθυνση. Συχνά χρησιμοποιούνται για να αναπαραστήσουν φυσικά μεγέθη όπως η ταχύτητα ή η δύναμη, που έχουν και μέγεθος και κατεύθυνση.
Τα διανύσματα μπορούν να αναπαρασταθούν γραφικά ως κατευθυνόμενα ευθύγραμμα τμήματα (βελάκια), με το μέγεθος του διανύσματος να αντιπροσωπεύεται από το μήκος του τμήματος και την κατεύθυνση του διανύσματος να αντιπροσωπεύεται από την κατεύθυνση του τμήματος. Τα διανύσματα μπορούν επίσης να αναπαρασταθούν μαθηματικά ως διατεταγμένα ζεύγη ή πλειάδες πραγματικών αριθμών, όπως (x, y), όπου τα x και y αντιπροσωπεύουν τα συστατικά του διανύσματος σε ένα δεδομένο σύστημα συντεταγμένων.
Χαρακτηριστικά των διανυσμάτων:
- Μέτρο διανύσματος
- Φορέας διανύσματος
- Ομόρροπα
- Αντίρροπα
- Το μηδενικό διάνυσμα
- Ίσα διανύσματα
- Αντίθετα διανύσματα
Διαφορά διανυσμάτων –
– 
Ονομάζουμε διαφορά – , του διανύσματος από το διάνυσμα το διάνυσμα + (-), όπου – το αντίθετο διάνυσμα του . Ισχύει: – = + (-)
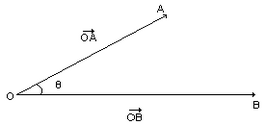
Γωνία δύο διανυσμάτων
Γωνία διανυσμάτων.Η θ είναι η γωνία που σχηματίζουν τα διανύσματα της εικόνας.
Γωνία δύο μη μηδενικών διανυσμάτων ονομάζουμε τη κυρτή γωνία που αυτά σχηματίζουν αν τα πάρουμε με κοινή αρχή και είναι ανεξάρτητη από την επιλογή του σημείου κοινής αρχής.
Εύρεση γωνίας από εσωτερικό γινόμενο:
Μπορεί να υπολογιστεί η γωνία μεταξύ δύο διανυσμάτων και εφαρμόζοντας την παρακάτω σχέση:
Θ = cos−1( / *)
/ 
*
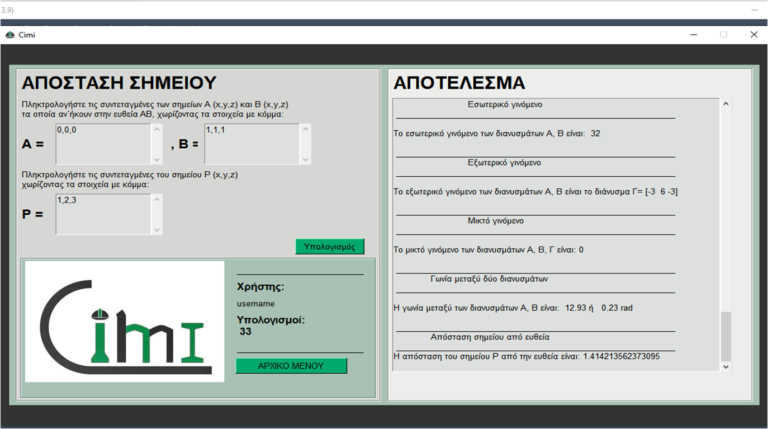
)Δοκιμάστε το Cimi
Δοκιμάστε το integral_calculator
Μικτό γινόμενο
Είναι ένας συνδυασμός των άλλων δύο (εσωτερικό και εξωτερικό γινόμενο). Στο μικτό γινόμενο έχουμε 3 διανύσματα και το αποτέλεσμα που προκύπτει είναι αριθμός.
Έστω τρία διανύσματα , και . Για τα τα τρία αυτά διανύσματα ισχύουν τα ακόλουθα:
- .
- Το ονομάζεται τριπλό βαθμωτό ή μικτό γινόμενο και υπολογίζεται από την ορίζουσα . Το γινόμενο αυτό εκφράζει τον όγκο του παραλληλεπιπέδου με πλευρές τα διανύσματα , και ή το αρνητικό τους στην περίπτωση όπου τα τρία αυτά διανύσματα δεν σχηματίζουν ένα δεξιόστροφο σύστημα συντεταγμένων.
- Το γινόμενο ονομάζεται τριπλό εξωτερικό γινόμενο.
Πρόσθεση διανυσμάτων
Έστω δύο διανύσματα και και ζητούμε το άθροισμα . Με αρχή ένα σημείο Ο παίρνουμε τα διανύσματα και . Το διάνυσμα λέγεται άθροισμα ή συνισταμένη των δύο διανυσμάτων. Το άθροισμα των διανυσμάτων αποδεικνύεται ότι είναι ανεξάρτητο από την επιλογή του σημείου Ο. Το άθροισμα δύο διανυσμάτων μπορεί να βρεθεί και με το λεγόμενο κανόνα του παραλληλογράμμου.
Εσωτερικό γινόμενο
Το εσωτερικό γινόμενο δύο διανυσμάτων και συμβολίζεται με και ορίζεται ως
όπου με και συμβολίζουμε τα μέτρα των διανυσμάτων και αντίστοιχα και θ τη γωνία που σχηματίζεται ανάμεσα στα δύο διανύσματα. Είναι φανερό πως το εσωτερικό γινόμενο δύο διανυσμάτων θα είναι πάντα ένας αριθμός και όχι ένα νέο διάνυσμα όπως στην πρόσθεση και την αφαίρεση διανυσμάτων.
Όταν τα διανύσματα είναι κάθετα μεταξύ τους, το εσωτερικό γινόμενο είναι ίσο με το 0, ενώ όταν είναι παράλληλα (ή αντιπαράλληλα) το εσωτερικό γινόμενο ισούται με το θετικό (ή αρνητικό αντίστοιχα) γινόμενο των μέτρων τους. Αυτό είναι φανερό γιατί και ή .
Το εσωτερικό γινόμενο χρησιμοποιείται εκτεταμένα στις εξισώσεις της φυσικής, όπως και όλος ο διανυσματικός λογισμός άλλωστε.
Δοκιμάστε το integral_calculator
Εξωτερικό γινόμενο
Το εξωτερικό γινόμενο δύο διανυσμάτων διαφέρει από το εσωτερικό γινόμενο όσον αφορά τα αποτελέσματα των πράξεων. Στο μεν εσωτερικό γινόμενο λαμβάνουμε ένα βαθμωτό μέγεθος ως αποτέλεσμα (αριθμό), ενώ στο εξωτερικό παίρνουμε ένα διάνυσμα.
Το εξωτερικό γινόμενο δεν γενικεύεται για n διαστάσεις, έχει νόημα μόνο σε τρισδιάστατους χώρους.
Αν και είναι τα δύο διανύσματα, το εξωτερικό γινόμενο συμβολίζεται ως και ορίζεται ως
και είναι τα μέτρα των διανυσμάτων και , sin θ το ημιτονο αυτών των διανυσμάτων, είναι η γωνία μεταξύ των δύο διανυσμάτων, και είναι το μοναδιαίο διάνυσμα κάθετο στο επίπεδο που ορίζουν τα και .
Γραφικά, το εξωτερικό γινόμενο αναπαρίσταται από το σχήμα, όπου φαίνεται ότι , δηλαδή στην πράξη του εξωτερικού γινομένου δεν ισχύει η αντιμεταθετική ιδιότητα. Τα φυσικά μεγέθη (διανύσματα) που παράγουν το νέο διάνυσμα γράφονται με συγκεκριμένη σειρά και η κατεύθυνση του εξωτερικού γινομένου προκύπτει με τον κανόνα του δεξιού χεριού .
Για παράλληλα ή αντιπαράλληλα διανύσματα το εξωτερικό γινόμενο δίνει το μηδενικό διάνυσμα, εφόσον και .
Το εξωτερικό γινόμενο δύο διανυσμάτων και μπορεί ακόμη να εκφραστεί με την μορφή ορίζουσας: |.
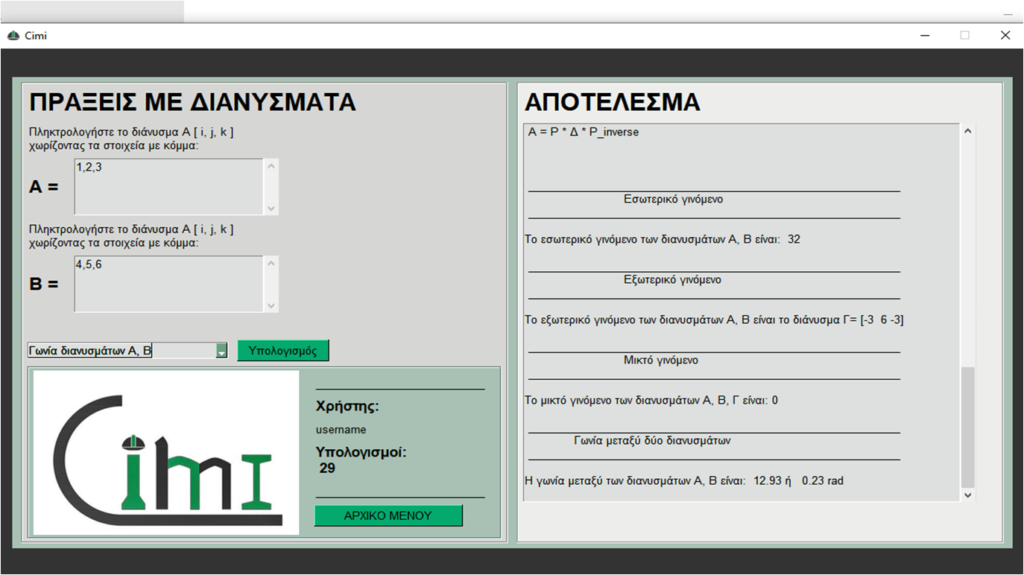
παραδειγματα
Στην παρακάτω εικόνα φαίνονται οι πράξεις των δύο διανυσμάτων Α = [1,2,3] , Β = [4,5,6] χρησιμοποιώντας το πρόγραμμα υπολογισμού Cimi.
ΙΔΙΟΤΙΜΕΣ - ΙΔΙΟΔΙΑΝΥΣΜΑΤΑ
Στη γραμμική άλγεβρα, η θεωρία ιδιοτιμών χρησιμοποιείται για τη μελέτη των γραμμικών μετασχηματισμών και των ιδιοτήτων τους. Η κύρια ιδέα πίσω από τη θεωρία ιδιοτιμών είναι η εύρεση χαρακτηριστικών τιμών (ιδιοτιμών) και αντίστοιχων διανυσμάτων (ιδιοδιανύσματα) που ικανοποιούν μια συγκεκριμένη μαθηματική ιδιότητα.
Με δεδομένο έναν τετραγωνικό πίνακα A και ένα μη μηδενικό διάνυσμα x, μια ιδιοτιμή λ και ένα ιδιοδιάνυσμα v λέγεται ότι ικανοποιούν την εξίσωση ιδιοτιμής Av = λv εάν πολλαπλασιάζοντας τον πίνακα A με το διάνυσμα v έχει ως αποτέλεσμα ένα κλιμακωτό πολλαπλάσιο του v , το διάνυσμα v είναι αμετάβλητο, αλλά το μέγεθός του πολλαπλασιάζεται επί λ.
Ονομάζουμε χαρακτηριστικό πολυώνυμο μιας γραμμικής απεικόνισης f το πολυώνυμο:
P ( λ ) = | Α – λΙ |
όπου Α ο πίνακας της f και Ι ο μοναδιαιος πίνακα. Οι ιδιοτιμές μιας γραμμικής απεικόνισης f είναι οι ρίζες του χαρακτηριστικού της πολυωνύμου
P ( λ ) = | Α – λΙ | = 0
Οι ιδιοτιμές και τα ιδιοδιανύσματα έχουν σημαντικές εφαρμογές σε πολλούς τομείς των μαθηματικών, της επιστήμης και της μηχανικής, όπως τα γραφικά υπολογιστών, η κβαντική μηχανική και η θεωρία ελέγχου. Χρησιμοποιούνται για τη μελέτη των ιδιοτήτων των γραμμικών μετασχηματισμών, για τη διαγώνοποιηση πινάκων και για την επίλυση συστημάτων γραμμικών εξισώσεων.
Μεθοδολογία
Μεθοδολογία υπολογισμού ιδιοτιμών και ιδιοδιανυσμάτων (2 βήματα):
- Εύρεση ορίζουσας | Α – λΙ | = 0. Οι τιμές του λ που θα βρεθούν ονομάζονται χαρακτηιστικές τιμές ή ιδιοτιμές και παριστάνουν τις διευθύνσεις.
- Για κάθε τιμη του λ που βρέθηκε υπολογίζονται τα αντίστοιχα ιδιοδιανύσματα V έτσι ώστε Αx = λx .
ΠΑΡΑΔΕΙΓΜΑ
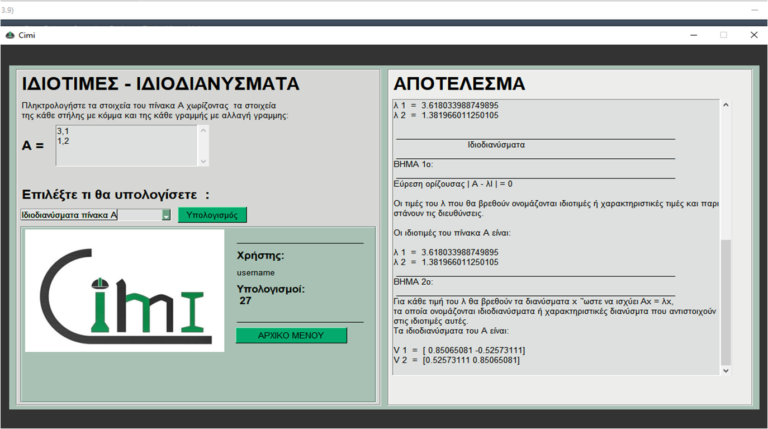
Στην παρακάτω εικόνα φαίνονται η διαδικασία υπολογισμού των ιδιοδιανυσμάτων του πίνακα Α = [3,1 ; 1,2 ] χρησιμοποιώντας το πρόγραμμα υπολογισμού Cimi.
ΔΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ
Η διαγωνοποίηση ενός πίνακα αναφέρεται στη διαδικασία εύρεσης ενός διαγώνιου πίνακα που είναι παρόμοιος με τον αρχικό πίνακα. Ένας διαγώνιος πίνακας είναι ένας τετραγωνικός πίνακας στον οποίο όλες οι τιμές πάνω και κάτω από την κύρια διαγώνιο είναι μηδέν.
Ένας τετραγωνικός πίνακας Α λέγεται ότι μπορεί να διαγωνοποιηθεί εάν και μόνο εάν υπάρχει ένας διαγώνιος πίνακας Δ και ένας αντιστρέψιμος πίνακας P έτσι ώστε:
A = P Δ P^(-1)
όπου P^(-1) είναι το αντίστροφο του P.
Η θεωρία της ιδιοτιμής σχετίζεται στενά με τη διαγωνοποίηση πινάκων. Εάν ένας πίνακας έχει n γραμμικά ανεξάρτητα ιδιοδιανύσματα, τότε ο πίνακας μπορεί να διαγωνοποιηθεί. Αυτά τα ιδιοδιανύσματα σχηματίζουν τις στήλες του πίνακα P και οι αντίστοιχες ιδιοτιμές τοποθετούνται στην κύρια διαγώνιο του πίνακα D.
Η διαγωνοποίηση έχει πολλές σημαντικές εφαρμογές στη γραμμική άλγεβρα και σε συναφή πεδία. Χρησιμοποιείται για την απλοποίηση του υπολογισμού των δυνάμεων του πίνακα, για την εύρεση του αντιστρόφου ενός πίνακα και για την επίλυση συστημάτων γραμμικών διαφορικών εξισώσεων, μεταξύ άλλων.
Μεθοδολογία
Μεθοδολογία υπολογισμού ιδιοτιμών και ιδιοδιανυσμάτων (2 βήματα):
- Εύρεση ιδιοτιμών του Α υπολογίζοντας την ορίζουσας= | Α – λΙ | = 0. Οι τιμές του λ που θα βρεθούν ονομάζονται χαρακτηιστικές τιμές ή ιδιοτιμές.
- Εύρεση ιδιοδιανυσμάτων για κάθε τιμη του λ που βρέθηκε. Υπολογίζονται τα αντίστοιχα ιδιοδιανύσματα V έτσι ώστε Αx = λx .
- Δημιουργία πίνακα Δ. Τοποθετούνται στην διαγώνιο του πίνακα οι ιδιοτιμές λ που βρέθηκαν στο βήμα 1.
- Δημιουργία πίνακα P. Τοποθετούνται στις στήλες του P τα ιδιοδιανύσματα V που βρέθηκαν στο βήμα 2.
- Εύρεση αντίστροφου πίνακα P