Περιεχόμενα:
- Εισαγωγή
- Σφάλματα – Ακρίβεια
- Μη γραμμικές εξισώσεις
- Επίλυση γραμμικών συστημάτων
- Ιδιοτιμές – ιδιοδιανύσματα
- Παρεμβολή
- Παραγώγιση
- Ολοκλήρωση

ΕΙΣΑΓΩΓΗ
Η αριθμητική ανάλυση είναι ένα συναρπαστικό πεδίο που ασχολείται με τη χρήση αριθμητικών μεθόδων για την επίλυση μαθηματικών προβλημάτων. Εάν ενδιαφέρεστε για αυτόν τον τομέα, τότε μπορεί να θέλετε να γνωρίσετε τον John, έναν αριθμητικό αναλυτή που εργάζεται σε αυτόν τον τομέα για πάνω από μια δεκαετία.
Ο John έχει ισχυρό υπόβαθρο στα μαθηματικά και την επιστήμη των υπολογιστών. Είναι παθιασμένος με την εύρεση λύσεων σε πολύπλοκα μαθηματικά προβλήματα χρησιμοποιώντας αριθμητικές μεθόδους. Ο John είναι ειδικευμένος σε διάφορους τομείς αριθμητικής ανάλυσης, συμπεριλαμβανομένης της αριθμητικής γραμμικής άλγεβρας, της βελτιστοποίησης και των αριθμητικών διαφορικών εξισώσεων.
Έχει μεγάλη εμπειρία στην ανάπτυξη αλγορίθμων και λογισμικού για την επίλυση αριθμητικών προβλημάτων. Ο John έχει εργαστεί σε πολλά έργα που περιλαμβάνουν αριθμητικές προσομοιώσεις για εφαρμογές πραγματικού κόσμου στη μηχανική, τη φυσική και τα οικονομικά.
Ο John είναι ειδικός στη χρήση MATLAB, Python και άλλων γλωσσών προγραμματισμού για αριθμητικούς υπολογισμούς. Γνωρίζει επίσης τους παράλληλους υπολογιστές, τους υπολογιστές υψηλών επιδόσεων και τους επιστημονικούς υπολογιστές.
Εάν ενδιαφέρεστε να μάθετε περισσότερα σχετικά με την αριθμητική ανάλυση ή χρειάζεστε βοήθεια για την επίλυση ενός αριθμητικού προβλήματος, ο John θα ήταν ένα εξαιρετικό άτομο για να απευθυνθείτε. Η τεχνογνωσία και η εμπειρία του τον καθιστούν πολύτιμο πόρο για όποιον ενδιαφέρεται για αυτόν τον συναρπαστικό τομέα.
Σφαλματα – Ακριβεια
Αριθμητική του υπολογιστή
Η αριθμητική του υπολογιστή είναι η διαδικασία εκτέλεσης μαθηματικών πράξεων, όπως πρόσθεση, αφαίρεση, πολλαπλασιασμός, διαίρεση, κ.α., χρησιμοποιώντας ηλεκτρονικές συσκευές που ονομάζονται υπολογιστές. Αυτές οι πράξεις μπορούν να εκτελεστούν σε διαφορετικά αριθμητικά συστήματα, όπως το δεκαδικό, το δυαδικό ή το δεκαεξαδικό αριθμητικό σύστημα.
Το δεκαδικό αριθμητικό σύστημα αποτελείται από τους αριθμούς που χρησιμοποιούμε στην καθημερινή ζωή, όπως 1, 2, 3, 10, 100 κ.λπ. Στην αριθμητική του υπολογιστή, οι δεκαδικοί αριθμοί αναπαρίστανται χρησιμοποιώντας το σύστημα βάσης-10. Το σύστημα βάσης-10 χρησιμοποιεί 10 ψηφία, από το 0 έως το 9, για να αναπαραστήσει αριθμούς. Κάθε ψηφίο ενός δεκαδικού αριθμού αντιπροσωπεύει μια δύναμη του 10, δηλαδή ότι πολλαπλασιάζεται επί το 10 υψωμένο σε δύναμη που αντιστοιχεί στην θέση του ψηφίου αυτού.
Για παράδειγμα, στον αριθμό 123, το ψηφίο 1 αντιπροσωπεύει το 100 (10 στη δύναμη του 2), το ψηφίο 2 αντιπροσωπεύει το 20 (10 στη δύναμη του 1) και το το ψηφίο 3 αντιπροσωπεύει το 3 (10 στη δύναμη του 0).
Για παράδειγμα:
83=(8 × 10^1) + (3 × 10^0)
1245=(1 × 10^3) + (2 × 10^2) + (4 × 10^1) + (5 ×10^0)
Το ίδιο ισχύει και για τους δεκαδικούς αριθμούς, αλλά χρησιμοποιούμε αρνητικές δυνάμεις του 10.
π.χ.
0,75=(7 × 10^(-1)) + (5 × 10^(-2))
Έτσι, ένας αριθμός με ακέραιο και δεκαδικό μέρος, έχει ψηφία υψωμένα σε θετικές και αρνητικές δυνάμεις της βάσης 10. π.χ.
134,95=(1 × 10^2) + (3 × 10^1) + (4 ×10^0) + (9 × 10^(-1)) + (5 × 10^(-2))
Με την ίδια λογική μπορείτε να υπολογίσετε την αξία ενός αριθμού (η οποία είναι ένας αριθμός σε δεκαδικό σύστημα) σε συστήματα με διαφορετική βάση από το 10 (π.χ. στο δυαδικό με βάση το 2, ή το δεκαεξαδικό με βάση το 16). Ο εκάστοτε αριθμός θα μετατραπεί έτσι στον αντίστοιχο στο δεκαδικό σύστημα, που είναι πιo κατανοητό από τους περισσότερους.
Το δυαδικό αριθμητικό σύστημα είναι ένα άλλο σύστημα αριθμών που χρησιμοποιείται στην αριθμητική υπολογιστών. Στο δυαδικό σύστημα, υπάρχουν μόνο δύο ψηφία, το 0 και το 1 και χρησιμοποιούνται από τον υπολογιστή για την αναπαράσταση αριθμών. Κάθε ψηφίο σε έναν δυαδικό αριθμό αντιπροσωπεύει μια δύναμη του 2. Για παράδειγμα, στον αριθμό 101, το ψηφίο 1 αντιπροσωπεύει το 4 (2 στη δύναμη του 2), το ψηφίο 0 αντιπροσωπεύει το 0 (2 στη δύναμη του 1) και το ψηφίο 1 αντιπροσωπεύει το 1 (2 στη δύναμη του 0). Οι δυαδικοί αριθμοί χρησιμοποιούνται συνήθως σε συστήματα υπολογιστών επειδή μπορούν εύκολα να αναπαρασταθούν χρησιμοποιώντας ηλεκτρονικά κυκλώματα.
Ο δυαδικός αριθμός (1101)2 αναπαριστά ποσότητα ίση με 1 μονάδα (1×2^0), 0 δυάδες (0×2^1), 1 τετράδα (1×2^2) και 1 οκτάδα (1×2^3) . Διαβάζεται : “ένα, ένα, μηδέν, ένα με βάση 2”. Ισούται δηλαδή με τον αριθμό 13 του δεκαδικού συστήματος,
1×2^0 + 0×2^1 + 1×2^2 + 1×2^3 = 13
Παρακάτω παρουσιάζεται μέσω παραδείγματος ένας απλός τρόπος μετατροπής φυσικών αριθμών από δεκαδική σε δυαδική μορφή.
Έστω ότι έχουμε τον αριθμό 1310, όπως στο αρχικό παράδειγμα. Γράφουμε τις δυνάμεις του 2, μέχρι να προκύψει αριθμός μεγαλύτερος ή ίσος από τον ζητούμενο αριθμό, οπότε σταματάμε στον αμέσως προηγούμενο.
2^0=1
2^1=2
2^2=4
2^3=8
Στην προκειμένη περίπτωση ο ζητούμενος αριθμός είναι το 13, άρα σταματάμε στο 2^3=8, γιατί 2^4 = 16 > 13. Παρατηρούμε ότι ο αριθμός 2^3 χωράει μια φορά στο 13, άρα σημειώνουμε x1. Το αποτέλεσμα της αφαίρεσης είναι 5. Το 2^2 χωράει μια φορά στο 5 άρα σημειώνουμε x1. Μένει 1 , όμως το 2%1 δε χωράει στο ένα άρα σημειώνουμε x0. Τέλος το 2^0 χωράει μια φορά στο ένα , άρα σημειώνουμε x1.
13
-2^3 x1
>5
-2^2 x1
>1
-2^1 x0
>1
-2^0 x1
>0
Γράφοντας τις σημειώσεις στη σειρά από πάνω ως κάτω, προκύπτει ο αριθμός σε δυαδική μορφή. Δηλαδή, 11012 = 1310. Με τον ίδιο τρόπο μπορούμε να μετατρέψουμε έναν δεκαδικό αριθμό σε οποιοδήποτε σύστημα, χρησιμοποιώντας κάθε φορά τις δυνάμεις της βάσης του εκάστοτε συστήματος αρίθμησης (οκταδικό, δεκαεξαδικό κτλ.).
Ένας δεύτερος επίσης απλός τρόπος για την μετατροπή ενός αριθμού από το δεκαδικό σύστημα αρίθμησης στο δυαδικό είναι
Βήμα 1 : διαιρούμε τον αριθμό με το 2 (ακέραια διαίρεση δηλ. δεν προχωράμε σε υποδιαστολή)
Βήμα 2 : Το πηλίκο που βρήκαμε το διαιρούμε με το 2
Πραγματοποιούμε επαναληπτικά το βήμα 2 εως ότου στο πηλίκο έχουμε 0
Τέλος παίρνουμε από κάτω προς τα πάνω (ανάποδα) τα υπόλοιπα των διαιρέσεων και έχουμε τον αριθμό στο δυαδικό σύστημα αρίθμησης.
Για να εκτελέσουν αριθμητικές πράξεις σε δεκαδικούς ή δυαδικούς αριθμούς, οι υπολογιστές χρησιμοποιούν λογικά κυκλώματα και αλγόριθμους που χειρίζονται αυτούς τους αριθμούς σύμφωνα με ορισμένους κανόνες. Για παράδειγμα, για να προσθέσετε δύο δεκαδικούς αριθμούς, ο υπολογιστής προσθέτει πρώτα τα δεξιά ψηφία και μεταφέρει οποιαδήποτε επιπλέον τιμή στην επόμενη στήλη. Στη συνέχεια επαναλαμβάνει αυτή τη διαδικασία για κάθε στήλη μέχρι να προστεθούν όλα τα ψηφία. Ομοίως, για να προσθέσει δύο δυαδικούς αριθμούς, ο υπολογιστής χρησιμοποιεί την ίδια διαδικασία, αλλά μεταφέρει οποιαδήποτε επιπλέον τιμή στην επόμενη στήλη όταν το άθροισμα είναι μεγαλύτερο από 1.
Μετατροπή αριθμών από το δεκαδικό στο δυαδικό σύστημα με το Matlab:
|
function binary = decimalToBinary(decNum) % DECIMALTOBINARY Convert decimal number to binary. % BINARY = DECIMALTOBINARY(DECNUM) converts the decimal number DECNUM % to binary and returns the binary number as a string. % % Example: % binary = decimalToBinary(10)
% Convert decimal number to binary using dec2bin() function binary = dec2bin(decNum);
% Display the binary representation of the decimal number disp([‘The binary representation of ‘, num2str(decNum), ‘ is ‘, binary]); End
|
To use this function, simply call it with a decimal number as the input argument: binary = decimalToBinary(10); The function will return the binary representation of the decimal number as a string: The binary representation of 10 is 1010
|
Το αντίστροφο: ΔΥΑΔΙΚΟ ΣΕ ΔΕΚΑΔΙΚΟ
|
function decNum = binaryToDecimal(binary) % BINARYTODECIMAL Convert binary number to decimal. % DECNUM = BINARYTODECIMAL(BINARY) converts the binary number BINARY % to decimal and returns the result as a numeric value. % Example: % decNum = binaryToDecimal(‘1010’) % Convert binary number to decimal using bin2dec() function decNum = bin2dec(binary); % Display the decimal representation of the binary number disp([‘The decimal representation of ‘, binary, ‘ is ‘, num2str(decNum)]); end
|
To use this function, simply call it with a binary number as the input argument: decNum = binaryToDecimal(‘1010’); The function will convert the binary number to decimal and return the result as a numeric value: The decimal representation of 1010 is 10
|
Σφαλματα
Στην αριθμητική ανάλυση, σφάλματα μπορεί να προκύψουν από διάφορες πηγές, όπως η ακρίβεια των μετρήσεων, οι περιορισμοί των υπολογιστικών πόρων ή οι προσεγγίσεις που γίνονται σε μαθηματικά μοντέλα. Η κατανόηση και η διαχείριση των σφαλμάτων είναι ζωτικής σημασίας για τη διασφάλιση της αξιοπιστίας και της εγκυρότητας των αριθμητικών υπολογισμών. Σε αυτό το κείμενο, θα γνωρίσετε τους πιο συνηθισμένους τύπους σφαλμάτων στην αριθμητική ανάλυση και πώς διαδίδονται μέσω υπολογισμών.
- Απόλυτο και σχετικό λάθος
- Σημαντικά ψηφία
- Σφάλμα απαλοιφής
- Σφάλμα συνάθροισης
- Σφάλμα αναπαράστασης
Όταν κάνετε μια μέτρηση ή μια προσέγγιση, συχνά δεν είναι δυνατό να ληφθεί η ακριβής τιμή της ποσότητας ενδιαφέροντος. Αντίθετα, λαμβάνουμε μια εκτίμηση που έχει κάποιο βαθμό σφάλματος. Το απόλυτο σφάλμα μιας εκτίμησης είναι η διαφορά μεταξύ της εκτίμησης και της πραγματικής τιμής, ενώ το σχετικό σφάλμα είναι το απόλυτο σφάλμα διαιρούμενο με την πραγματική τιμή. Για παράδειγμα, αν υπολογίσουμε την τιμή του π να είναι 3,14,
- το απόλυτο σφάλμα είναι |π – 3,14| και
- το σχετικό σφάλμα είναι |π – 3,14| / |π|.
Το σχετικό σφάλμα εκφράζεται συχνά ως ποσοστό. Σε αυτό το παράδειγμα το π είναι η πραγματική τιμή και το 3,14 είναι η εκτίμηση (προσεγγιστική τιμή)
Σημαντικά ψηφία είναι τα ψηφία που φέρουν νόημα σε μια αριθμητική τιμή. Κατά την εκτέλεση υπολογισμών, πρέπει να λαμβάνουμε υπόψη τα σημαντικά ψηφία των τιμών εισόδου για να αποφύγουμε την εισαγωγή πρόσθετου σφάλματος. Ο εμπειρικός κανόνας είναι ότι το αποτέλεσμα ενός υπολογισμού δεν πρέπει να έχει πιο πολλά σημαντικά ψηφία από την τιμή εισόδου με τα λιγότερα σημαντικά ψηφία. Για παράδειγμα, αν προσθέσουμε 1,23 και 4,567, θα πρέπει να στρογγυλοποιήσουμε το αποτέλεσμα σε δύο δεκαδικά ψηφία, αφού το 1,23 έχει μόνο δύο σημαντικά ψηφία.
Το σφάλμα απαλοιφής εμφανίζεται όταν αφαιρέσουμε δύο σχεδόν ίσους αριθμούς. Λόγω της περιορισμένης ακρίβειας της αριθμητικής του υπολογιστή, το αποτέλεσμα μπορεί να έχει μεγάλο σχετικό σφάλμα, ακόμη και αν το απόλυτο σφάλμα είναι μικρό. Αυτό συμβαίνει επειδή τα σημαντικά στοιχεία στους δύο αριθμούς ακυρώνονται, αφήνοντας μόνο τα λιγότερο σημαντικά ψηφία. Για να αποφύγουμε το σφάλμα απαλοιφής, μπορούμε να χρησιμοποιήσουμε εναλλακτικές μεθόδους, όπως η αναδιάταξη της εξίσωσης ή η χρήση διαφορετικής αναπαράστασης των αριθμών.
Συμπέρασμα: όταν υπάρχει σφάλμα απαλοιφής, υπάρχει και απώλεια σημαντικών ψηφίων. Όσο μεγαλύτερη είναι η ακρίβεια που χρησιμοποιεί ο υπολογιστής τόσο μικρότερο είναι το σφάλμα απαλοιφής.
Σφάλμα συνάθροισης παρουσιάζεται όταν προσθέτουμε μεγάλο αριθμό τιμών, ιδιαίτερα αν μερικές από αυτές είναι πολύ μικρές. Λόγω της περιορισμένης ακρίβειας της αριθμητικής του υπολογιστή, το συσσωρευμένο σφάλμα μπορεί να γίνει σημαντικό. Αυτό συμβαίνει επειδή τα σημαντικά ψηφία στις μικρές τιμές μπορεί να χαθούν λόγω στρογγυλοποίησης ή περικοπής. Για να ελαχιστοποιήσουμε το σφάλμα συνάθροισης, μπορούμε να χρησιμοποιήσουμε εναλλακτικές μεθόδους, όπως η αναδιάταξη της σειράς της άθροισης ή η χρήση ενός πιο ακριβούς αλγόριθμου.
Σφάλμα αναπαράστασης παρουσιάζεται όταν αναπαριστάνουμε έναν πραγματικό αριθμό χρησιμοποιώντας έναν πεπερασμένο αριθμό ψηφίων, όπως σε έναν υπολογιστή. Λόγω της περιορισμένης ακρίβειας της αριθμητικής του υπολογιστή, η αναπαράσταση μπορεί να μην είναι ακριβής και η τιμή μπορεί να είναι στρογγυλοποιημένη ή περικομμένη. Αυτό μπορεί να δημιουργήσει πρόσθετο σφάλμα στους υπολογισμούς, ιδιαίτερα εάν ο αριθμός έχει πολλά σημαντικά ψηφία ή εάν οι αριθμητικές πράξεις είναι ευαίσθητες στη στρογγυλοποίηση. Για να ελαχιστοποιήσουμε το σφάλμα αναπαράστασης, μπορούμε να χρησιμοποιήσουμε εναλλακτικές αναπαραστάσεις, όπως αριθμητική αυθαίρετης ακρίβειας ή αριθμητική διαστήματος.
Συμπερασματικά, τα σφάλματα αποτελούν εγγενές μέρος της αριθμητικής ανάλυσης και η κατανόηση της φύσης και της διάδοσής τους είναι απαραίτητη για τη διασφάλιση της ακρίβειας και της αξιοπιστίας των υπολογιστικών αποτελεσμάτων. Εφαρμόζοντας κατάλληλες τεχνικές και αλγόριθμους, μπορούμε να ελαχιστοποιήσουμε τα σφάλματα και να αποκτήσουμε ουσιαστικές και αξιόπιστες αριθμητικές λύσεις.
Ακριβεια
Στην αριθμητική ανάλυση, η ακρίβεια και η αριθμητική ακρίβεια είναι σημαντικές έννοιες που πρέπει να λαμβάνονται υπόψη κατά την εκτέλεση υπολογισμών.
- Η ακρίβεια αναφέρεται στον αριθμό των ψηφίων που χρησιμοποιούνται για την αναπαράσταση μιας ποσότητας, ενώ
- Η αριθμητική ακρίβεια αναφέρεται στο πόσο κοντά είναι μια υπολογισμένη τιμή στην πραγματική τιμή.
Προκειμένου να επιτευχθεί υψηλή ακρίβεια, είναι σημαντικό να χρησιμοποιείτε αρκετά ψηφία για να αναπαραστήσετε μια ποσότητα χωρίς να χάσετε σημαντικά ψηφία. Αυτό μπορεί να επιτευχθεί με τη χρήση κατάλληλων τεχνικών στρογγυλοποίησης και την αποφυγή σφαλμάτων περικοπής.
Η ακρίβεια, από την άλλη πλευρά, μπορεί να επηρεαστεί από διάφορους παράγοντες όπως τα σφάλματα μέτρησης, τα σφάλματα στρογγυλοποίησης και τα σφάλματα περικοπής. Για να βελτιωθεί η ακρίβεια, είναι σημαντικό να ελαχιστοποιηθούν αυτά τα σφάλματα και να χρησιμοποιηθούν κατάλληλες αριθμητικές μέθοδοι.
Ένας τρόπος μέτρησης της ακρίβειας ενός υπολογισμού είναι η χρήση απόλυτου σφάλματος και σχετικού σφάλματος. Όσο μικρότερα είναι τα απόλυτα και τα σχετικά σφάλματα, τόσο πιο ακριβής είναι ο υπολογισμός.
Ένας άλλος σημαντικός παράγοντας που πρέπει να ληφθεί υπόψη στην αριθμητική ανάλυση είναι η αριθμητική σταθερότητα. Ένας υπολογισμός λέγεται ότι είναι αριθμητικά σταθερός εάν μικρές αλλαγές στα δεδομένα εισόδου οδηγούν σε μικρές αλλαγές στην έξοδο. Αυτό είναι σημαντικό για να διασφαλιστεί ότι τα υπολογισμένα αποτελέσματα είναι αξιόπιστα και συνεπή.
Συνολικά, η ακρίβεια και η αριθμητική ακρίβεια είναι σημαντικές έννοιες που πρέπει να ληφθούν υπόψη στην αριθμητική ανάλυση για την εξασφάλιση αξιόπιστων και ακριβών υπολογισμών. Με την ελαχιστοποίηση των σφαλμάτων και τη χρήση κατάλληλων αριθμητικών μεθόδων, είναι δυνατό να επιτευχθεί υψηλή ακρίβεια και ακρίβεια στους υπολογισμούς.
Αλγοριθμοι
Ένας αλγόριθμος είναι ένα σύνολο οδηγιών που περιγράφει τον τρόπο επίλυσης ενός προβλήματος ή εκτέλεσης μιας εργασίας. Είναι μια διαδικασία βήμα προς βήμα που περιγράφει μια σειρά από πράξεις που πρέπει να εκτελεστούν προκειμένου να επιτευχθεί ένας συγκεκριμένος στόχος.
Οι αλγόριθμοι χρησιμοποιούνται σε διάφορους τομείς όπως τα μαθηματικά, η επιστήμη των υπολογιστών και η μηχανική, και είναι απαραίτητοι για την αποτελεσματική επίλυση πολύπλοκων προβλημάτων. Μπορούν να εκφραστούν με ποικίλες μορφές, όπως φυσική γλώσσα, ψευδοκώδικα, διαγράμματα ροής και γλώσσες προγραμματισμού.
Τα βασικά χαρακτηριστικά ενός αλγορίθμου είναι ότι πρέπει να είναι σαφής και να παράγει ένα σωστό αποτέλεσμα για όλες τις έγκυρες εισόδους. Επιπλέον, ένας αλγόριθμος θα πρέπει να είναι αποτελεσματικός, που σημαίνει ότι θα πρέπει να λύνει το πρόβλημα σε εύλογο χρονικό διάστημα και θα πρέπει να είναι εύκολο να κατανοηθεί και να εφαρμοστεί.
Υπάρχουν πολλά παραδείγματα αλγορίθμων στην καθημερινή ζωή, όπως συνταγές μαγειρικής, οδηγίες για τη συναρμολόγηση επίπλων ή ακόμα και μια ρουτίνα προπόνησης. Στην επιστήμη των υπολογιστών, οι αλγόριθμοι χρησιμοποιούνται για εργασίες όπως η ταξινόμηση δεδομένων, η αναζήτηση πληροφοριών και η επίλυση μαθηματικών προβλημάτων.
Συνολικά, οι αλγόριθμοι είναι ένα απαραίτητο εργαλείο για την επίλυση προβλημάτων και την αποτελεσματική και ακριβή εκτέλεση εργασιών. Ακολουθώντας ένα σύνολο καλά καθορισμένων βημάτων, ένας αλγόριθμος μπορεί να παρέχει μια αξιόπιστη και επαναλαμβανόμενη λύση σε ένα ευρύ φάσμα προβλημάτων.
Μη γραμμικες εξισωσεις
Οι μέθοδοι είναι επαναληπτικές και σε κάθε επανάληψη υπολογίζεται το απλό ή το σχετικό σφάλμα. Αν επιθυμείται ακρίβεια d τότε θα πρέπει να ισχύει η σχέση: |Ε|<=0,5*10^(-d)
Ενώ το προσεγγιστικό σφάλμα με πλήθος σημαντικών ψηφίων m |ε| <= 5*10^(-m)
Περιεχόμενα –
Μη γραμμικές εξισώσεις :
- Μέθοδος διχοτόμησης
- Μέθοδος Newton
- Μέθοδος της τέμνουσας (Regula falsi)
- Μέθοδος μεταβαλλόμενης χορδής (modified Regula falsi)
Η μέθοδος διχοτόμησης είναι μια αριθμητική τεχνική που χρησιμοποιείται για την εύρεση των ριζών μιας συνεχούς συνάρτησης. Είναι μια απλή και αξιόπιστη μέθοδος που στηρίζεται στο θεώρημα του Bolzano και μπορεί να χρησιμοποιηθεί για την προσέγγιση των ριζών μιας συνάρτησης με οποιονδήποτε βαθμό ακρίβειας επιθυμείτε.
Η μέθοδος διχοτόμησης λειτουργεί περιορίζοντας επαναληπτικά το εύρος στο οποίο βρίσκεται η ρίζα της συνάρτησης. Ξεκινά με ένα διάστημα που περιέχει τη ρίζα και στη συνέχεια διαιρεί αυτό το διάστημα στη μέση σε κάθε επανάληψη. Στη συνέχεια, αξιολογεί τη συνάρτηση στο μέσο του διαστήματος και καθορίζει σε ποιο μισό διάστημα πρέπει να βρίσκεται η ρίζα. Αυτή η διαδικασία επαναλαμβάνεται έως ότου το διάστημα είναι αρκετά μικρό ώστε να παραχθεί μια προσέγγιση της ρίζας που είναι αρκετά ακριβής για το επιθυμητό επίπεδο ακρίβεια.
Η μέθοδος της διχοτόμησης ακολουθεί τα παρακάτω 3 βήματα:
- Βήμα 1ο:
Εφαρμόζεται στο διάστημα [α, b] το θεώρημα του Bolzano και αν ισχύει f(a)*f(b) < 0 τότε διχοτομείται το διάστημα [α, b].
- Βήμα 2ο:
Θεωρώντας ότι α1 = α, b1 = b και ότι m είναι το μέσο του διαστήματος [α, b], άρα:
m= (α +b)/2 έχουμε:
Αν:
f(m)*f(α) < 0 τότε το f(b) = f(m)
f(m)*f(b) < 0 τότε το f(α) = f(m)
f(m) = 0 τότε m = ρίζα της f στο διάστημα [α, b]
- Βήμα 3ο:
Επαναλαμβάνεται την διαδικασία για το νέο διάστημα που βρήκατε στο βήμα 2
Η μέθοδος της διχοτόμησης συγκλίνει γραμμικά με ρυθμό 0,5 |r-cn|<= (0.5^(n))*(b-a). Επίσης μπορείτε να εκτιμήσετε τον μέγιστο αριθμό επαναλήψεων από την σχέση n>= (1/ln2)*ln(|a –b|/E). Τέλος σε κάθε επανάληψη θα πρέπει να υπολογίζεται το σφάλμα για την ακρίβεια.
Παράδειγμα, θεωρήστε τη συνάρτηση f(x) = x^3 – 4x – 9. Η μέθοδος διχοτόμησης μπορεί να χρησιμοποιηθεί για να βρεθεί η ρίζα αυτής της συνάρτησης μεταξύ x = 2 και x = 4.
Στην πρώτη επανάληψη,
- Βήμα 1: Εφαρμόζεται το θεώρημα του Bolzano για το διάστημα [2,4] : f(2)*f(4)<0 άρα το διάστημα διχοτομείται.
- Βήμα 2: Το μέσο του διαστήματος [2,4] είναι m = (2+4)/2 = 3. Η συνάρτηση που αξιολογείται σε αυτό το σημείο είναι f(3) = 27 – 12 – 9 = 6,
f(3)* f(2)<0 άρα το f(b) = f(m) και το νέο διάστημα είναι το [2,3].
Δεύτερη επανάληψη,
Το μέσο αυτού του διαστήματος είναι m = 2,5 και η συνάρτηση που αξιολογείται σε αυτό το σημείο είναι f(2,5) = 15,625 – 10 – 9 = -3,375.
f(2,5)* f(3)<0 άρα το f(α) = f(m) και το νέο διάστημα στο οποίο πρέπει να βρίσκεται η ρίζα είναι το [2.5,3].
Αυτή η διαδικασία συνεχίζεται έως ότου το διάστημα είναι αρκετά μικρό για να παραχθεί μια προσέγγιση της ρίζας που είναι αρκετά ακριβής για το επιθυμητό επίπεδο ακρίβειας.
Η μέθοδος διχοτόμησης είναι μια αξιόπιστη και στιβαρή τεχνική που μπορεί να χρησιμοποιηθεί για την εύρεση των ριζών ενός ευρέος φάσματος λειτουργιών. Είναι απλό στην εφαρμογή του και δεν απαιτεί καμία γνώση της παραγώγου της συνάρτησης. Ωστόσο, μπορεί να καθυστερήσει να συγκλίνει, ιδιαίτερα για συναρτήσεις που έχουν πολλές ρίζες ή ρίζες που είναι πολύ κοντά μεταξύ τους. Σε αυτές τις περιπτώσεις, πιο προηγμένες μέθοδοι όπως η μέθοδος του Newton μπορεί να είναι πιο κατάλληλες.
Κώδικας Matlab:
Στην αριστερή στήλη βρίσκεται ο κώδικας matlab για τη μέθοδο της διχοτόμησης και είναι γραμμένος στη μορφή συνάρτησης με όνομα bisection_method η συνάρτηση αυτή δέχεται 5 ορίσματα τα οποία είναι:
- η συνάρτηση f
- το άκρο α
- το άκρο β
- η ανοχή και
- ο μέγιστος αριθμός επαναλήψεων
Στην δεξιά στήλη βρίσκετε ένα παράδειγμα αυτής της μεθόδου για την συνάρτηση x^3 – 4*x – 9;
|
|
Για να χρησιμοποιήσετε αυτήν τη συνάρτηση, θα πρέπει να ορίσετε τη συνάρτηση f(x) της οποίας θέλετε να βρείτε τη ρίζα της και στη συνέχεια να καλέσετε τη συνάρτηση bisection_method με τις κατάλληλες εισόδους, ως εξής: |
|
function [root, iterations] = bisection_method(f, a, b, tol, max_iter) % Inputs: % – f: the function to find the root of % – a, b: the interval to search for the root in % – tol: the desired tolerance for the root % – max_iter: the maximum number of iterations to perform % Outputs: % – root: the approximate root of the function % – iterations: the number of iterations performed % Check that the function has different signs at the endpoints if sign(f(a)) == sign(f(b)) error(‘Function has same sign at endpoints, cannot use bisection method.’) end % Initialize variables iterations = 0; fa = f(a); root = a + (b-a)/2; error = abs(b-a)/2;
% Loop until the root is found or the maximum number of iterations is reached while error > tol && iterations < max_iter it erations = iterations + 1; fr = f(root); if sign(fr) == sign(fa) a = root; fa = fr; else b = root; end prev_root = root; root = a + (b-a)/2; error = abs(root – prev_root); end
% Display error message if maximum iterations reached if iterations == max_iter warning(‘Maximum number of iterations reached.’) end
|
f = @(x) x^3 – 4*x – 9; a = 2; b = 4; tol = 1e-6; max_iter = 100;
[root, iterations] = bisection_method(f, a, b, tol, max_iter);
fprintf(‘Approximate root: %f\n’, root); fprintf(‘Number of iterations: %d\n’, iterations); |
Η μέθοδος της διχοτόμησης συγκλίνει πολύ αργά, ειδικά αν το αρχικό διάστημα [α, β] στο οποίο αναζητούμε τη ρίζα είναι πολύ διευρυμένο. Η μέθοδος Newton χρησιμοποιεί την πρώτη παράγωγο της συνάρτησης f(x) για να προσεγγίσει τη ρίζα της και λόγω αυτού συγκλίνει ταχύτερα, αλλά υστερεί σε ακρίβεια. Στηρίζεται στην εφαρμογή του αναπτύγματος Taylor της συνάρτησης f(x) σε μια περιοχή του σημείου rε[α,β] εφαρμόζοντας τις λύσεις όπου η συνάρτηση είναι 2 φορές παραγωγίσιμη. Η μέθοδος Newton συγκλίνει υπερ γραμμικά.
Ακολουθεί η μεθοδολογία της μεθόδου:
- Ξεκινήστε με μια αρχική εικασία για τη ρίζα της εξίσωσης, που συμβολίζεται με x₀.
- Να αξιολογήσετε τη συνάρτηση f(x) και την παράγωγό της f'(x) σε x0.
- Χρησιμοποιήστε τον τύπο: x1 = x0 – (f(x₀) / f'(x₀)) για να υπολογίσετε μια νέα προσέγγιση, x1.
- Επαναλάβετε τα βήματα 2 και 3 μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας ή έως ότου επιτευχθεί ένας μέγιστος αριθμός επαναλήψεων.
- Η τελική τιμή του x, που συμβολίζεται ως xₙ, θα είναι η κατά προσέγγιση ρίζα της εξίσωσης.
Επαναλαμβάνοντας αυτή τη διαδικασία μπορούμε να υπολογίσουμε διαδοχικά σημεία τα οποία θα συγκλίνουν στη ρίζα. Υπάρχουν διάφοροι τρόποι που μπορούμε να επιλέξουμε για να καθορίσουμε το κριτήριο τερματισμού της μεθόδου. Μπορούμε να επιλέξουμε μια ανοχή tol > 0 και να υπολογίσουμε τα r1, r2, … , rn κάποια από τα παρακάτω κριτήρια να ικανοποιηθούν :
- η σύγκλιση ή μη της μεθόδου μπορεί να χαρακτηριστεί από τα παρακάτω:
- την επιλογή της κατάλληλης αρχικής τιμής που ακόμα και για γειτονικές θέσεις της συνάρτησης μπορεί να επιταχύνει τη σύγκλιση ή να ωθήσει σε απόκλιση της μεθόδου.
- Επίσης αν η συνάρτηση δεν είναι ομαλή στην περιοχή της ρίζας συνήθως αποκλίνει
Για τη σύγκλιση ισχύουν και 2 θεωρήματα:
- εάν μια συνάρτηση f(x) έχει συνεχή δεύτερη παράγωγο στην περιοχή της ρίζας και η ρίζα αυτή είναι απλή τότε υπάρχει μια περιοχή αρκετά κοντά στη ρίζα τέτοια ώστε με οποιοδήποτε xo που ανήκει στην περιοχή αυτή η ακολουθία συγκλίνει.
- Αν η f(x) έχει συνεχή δεύτερη παράγωγο σε ένα διάστημα [a,b] ισχύουν :
- η πρώτη παράγωγος f’(x) δεν μηδενίζεται στο [a,b]
- η δεύτερη παράγωγος f’’(x) έχει σταθερό πρόσημο στο διάστημα [a,b]
- ικανοποιείται το κριτήριο του Bolzano f(a) * f(b) <0
- ισχύει max{ f(a)/f’(a) , f(b)/f’(b) } <= b-a
αν δεν ικανοποιείται διχοτόμου με το αντίστοιχο διάστημα και εξετάζουμε σε ποιο από τα 2 διαστήματα ικανοποιούνται όλες τις συνθήκες.
Ακολουθεί ένα παράδειγμα για την επεξήγηση της μεθόδου Newton-Raphson:
Παράδειγμα 1:
Ας βρούμε μια προσέγγιση για τη ρίζα της εξίσωσης f(x) = x² – 4x – 10.
- Βήμα 1: Επιλέξτε μια αρχική εικασία, ας πούμε x₀ = 3.
- Βήμα 2: Αξιολογήστε τη συνάρτηση και την παράγωγό της σε x₀:
f(x0) = (3)² – 4(3) – 10 = -8
f'(x0) = 2(3) – 4 = 2
- Βήμα 3: Υπολογίστε μια νέα προσέγγιση χρησιμοποιώντας τον τύπο:
x1 = x0 – (f(x0) / f'(x₀)) = 3 – (-8 / 2) = 7
- Βήμα 4: Επαναλάβετε τα βήματα 2 και 3 με x1 ως νέα εικασία:
f(x1) = (7)² – 4(7) – 10 = 9
f'(x1) = 2(7) – 4 = 10
x2 = x1 – (f(x1) / f'(x1)) = 7 – (9 / 10) = 6,1
Επαναλάβετε αυτά τα βήματα μέχρι να επιτευχθεί η επιθυμητή ακρίβεια ή να επιτευχθεί ένας μέγιστος αριθμός επαναλήψεων. Η τελική τιμή που προκύπτει θα είναι η κατά προσέγγιση ρίζα της εξίσωσης.
Λάβετε υπόψη ότι η μέθοδος Newton-Raphson μπορεί να μην συγκλίνει πάντα ή μπορεί να συγκλίνει σε ένα τοπικό ελάχιστο. Είναι σημαντικό να επιλέξετε μια κατάλληλη αρχική εικασία και να γνωρίζετε τη συμπεριφορά της συνάρτησης.
Σε αυτόν τον κώδικα, ορίζουμε τη συνάρτηση f και την παράγωγό της df ως ανώνυμες συναρτήσεις χρησιμοποιώντας λαβές συναρτήσεων. Στη συνέχεια, ορίζουμε την αρχική εικασία x0, τον μέγιστο αριθμό επαναλήψεων maxIterations και την ανοχή ανοχής για σύγκλιση.
Ο βρόχος while εκτελεί την επανάληψη Newton-Raphson μέχρι η τιμή της συνάρτησης να είναι κάτω από την ανοχή ή να επιτευχθεί ο μέγιστος αριθμός επαναλήψεων. Μέσα σε κάθε επανάληψη, η νέα προσέγγιση x ενημερώνεται χρησιμοποιώντας τον τύπο x = x – f(x) / df(x).
Μετά τον βρόχο, ο κώδικας ελέγχει εάν η μέθοδος σύγκλινε ή έφτασε στον μέγιστο αριθμό επαναλήψεων και εμφανίζει το αντίστοιχο μήνυμα. Εάν η μέθοδος συγκλίνει, εμφανίζει την κατά προσέγγιση ρίζα της εξίσωσης.
Μπορείτε να τροποποιήσετε τον κώδικα αλλάζοντας τη συνάρτηση f, την παράγωγό της df, την αρχική εικασία x0 και άλλες παραμέτρους για να τον προσαρμόσετε στη συγκεκριμένη εξίσωσή σας.
ΚΩΔΙΚΑΣ MATLAB
|
% Function definition: f(x) = x^2 – 4x – 10 f = @(x) x^3 – 6*x +4;
% Derivative of the function: f'(x) = 2x – 4 df = @(x) 3*x^2 – 6;
% Initial guess x0 = 0.5;
% Maximum number of iterations maxIterations = 20;
% Tolerance for convergence tolerance = 1e-6;
% Initialize variables x = x0; iteration = 0;
% Newton-Raphson iteration while abs(f(x)) > tolerance && iteration < maxIterations x = x – f(x) / df(x); iteration = iteration + 1; end
% Check if method converged or reached maximum iterations if iteration == maxIterations disp(‘Maximum iterations reached. The method may not have converged.’); else disp([‘Root approximation: x = ‘, num2str(x)]); end
|
Root approximation: x = 0.73205 |
Αυτή η μέθοδος χρησιμοποιείται για την εύρεση της ρίζας μιας συνάρτησης προσεγγίζοντάς την ως το σημείο τομής μιας τεμνόμενης γραμμής με τον άξονα x. Η γραμμή τομής σχηματίζεται συνδέοντας δύο σημεία στην καμπύλη συνάρτησης.
Σημειώσεις
- Απαιτούνται 2 αρχικά σημεία xo, x
- Χρειάζονται περισσότερες επαναλήψεις από την λούτον για να συγκλίνει.
- Συγκλίνει γραμμικά και γίνεται όλο και πιο αργή (το ένα άκρο δεν κουνιέται καθόλου).
Μεθοδολογία:
- **Αρχική εικασία**: Επιλέξτε δύο αρχικά σημεία, x0 και x1, έτσι ώστε τα f(x0) και f(x1) να έχουν αντίθετα πρόσημα. Αυτά τα σημεία πρέπει να είναι κοντά στη ρίζα.
- **Γραμμή τέμνουσας**: Υπολογίστε την εξίσωση της γραμμής τομής που διέρχεται από τα σημεία (x0, f(x0)) και (x1, f(x1)). Η εξίσωση της τέμνουσας γραμμής δίνεται από:
y = f(x0) + (x – x0) * (f(x1) – f(x0)) / (x1 – x0)
- **Τομή**: Λύστε την εξίσωση y = 0 για να βρείτε τη συντεταγμένη x του σημείου όπου η τέμνουσα ευθεία τέμνει τον άξονα x. Αυτή η συντεταγμένη x είναι μια βελτιωμένη προσέγγιση της ρίζας.
- **Ενημέρωση**: Ενημερώστε τα σημεία (x0, f(x0)) και (x1, f(x1)) μετατοπίζοντάς τα προς τη νέα προσέγγιση. Έστω x0 = x1 και x1 = νέα προσέγγιση.
- **Σύγκλιση**: Επαναλάβετε τα βήματα 2-4 μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας ή έως ότου επιτευχθεί ένας μέγιστος αριθμός επαναλήψεων.
Παράδειγμα:
Ας βρούμε τη ρίζα της συνάρτησης f(x) = x^3 – 2x – 5 χρησιμοποιώντας τη μέθοδο χορδής.
- **Αρχική εικασία**: Επιλέξτε δύο αρχικά σημεία, x0 = 2 και x1 = 3. Αυτά τα σημεία ικανοποιούν f(x0) = -1 και f(x1) = 10, υποδεικνύοντας μια αλλαγή πρόσημου.
- **Γραμμή τέμνουσας**: Η εξίσωση της τμηματικής γραμμής που διέρχεται από (x0, f(x0)) και (x1, f(x1)) είναι:
y = -1 + (x – 2) * (10 – (-1)) / (3 – 2)
- **Τομή**: Λύστε την εξίσωση y = 0 για να βρείτε τη συντεταγμένη x του σημείου τομής. Σε αυτή την περίπτωση, λύνουμε -1 + (x – 2) * (10 – (-1)) / (3 – 2) = 0 για να λάβουμε x ≈ 2,272727272727273.
- **Ενημέρωση**: Ενημερώστε τα σημεία x0 και x1 ορίζοντας x0 = 3 και x1 = 2,272727272727273.
- **Σύγκλιση**: Επαναλάβετε τα βήματα 2-4 μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας ή έως ότου επιτευχθεί ένας μέγιστος αριθμός επαναλήψεων.
Ακολουθεί μια περίληψη των επαναλήψεων:
- Επανάληψη 1: x0 = 3, x1 = 2,272727272727273, Τομή ≈ 2,272727272727273
- Επανάληψη 2: x0 = 2,272727272727273, x1 = 2,006711409395973, Τομή ≈ 2,006711409395973
- Επανάληψη 3: x0 = 2,006711409395973, x1 = 2,001667561619582, Τομή ≈ 2,001667561619582
- Επανάληψη 4: x0 = 2,001667561619582, x1 = 2,001639210417746, Τομή ≈ 2,001639210417746
Μετά από μερικές επαναλήψεις, λάβαμε μια βελτιωμένη προσέγγιση της ρίζας ως x ≈ 2,001639210417746. Μπορούμε να συνεχίσουμε τις επαναλήψεις μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας.
Η μέθοδος της χορδής βελτιώνει επαναληπτικά την προσέγγιση της ρίζας κατασκευάζοντας τομείς και βρίσκοντας το σημείο τομής τους με τον άξονα x. Παρέχει έναν απλό και αποτελεσματικό τρόπο προσέγγισης της ρίζας μιας συνάρτησης.
Είναι σημαντικό να σημειωθεί ότι η μέθοδος της χορδής μπορεί να μην συγκλίνει πάντα ή να συγκλίνει αργά εάν η συνάρτηση έχει ορισμένα χαρακτηριστικά, όπως να είναι επίπεδη κοντά στη ρίζα ή να έχει πολλές ρίζες μέσα στο αρχικό διάστημα. Σε τέτοιες περιπτώσεις, άλλες μέθοδοι όπως το Newton-Raphson ή η διχοτόμηση μπορεί να είναι πιο κατάλληλες.
|
function |
output |
|
% Define the function f(x) f = @(x) x^2 – 2;
% Set initial guesses and other parameters x0 = 1; x1 = 2; max_iterations = 20; tolerance = 0.001;
% Call the chord_method function root = chord_method(f, x0, x1, max_iterations, tolerance); disp(root); % Display the approximate root
function root = chord_method(f, x0, x1, max_iterations, tolerance) % f: Function handle for the function f(x) % x0, x1: Initial guesses for the root % max_iterations: Maximum number of iterations % tolerance: Desired tolerance for the root approximation
% Initialize variables iteration = 0; error = inf;
% Perform chord iterations while error > tolerance && iteration < max_iterations % Compute the next approximation using the chord method x = x1 – (f(x1) * (x1 – x0)) / (f(x1) – f(x0));
% Calculate the error error = abs(x – x1);
% Update variables for the next iteration x0 = x1; x1 = x;
% Increment the iteration count iteration = iteration + 1; end
% Check convergence if iteration == max_iterations && error > tolerance disp(‘Chord method did not converge within the specified number of iterations.’); else disp(‘Chord method converged to the root:’); root = x; end end
|
Chord method converged to the root: 1.4142 |
Η μέθοδος μεταβαλλόμενης χορδής, γνωστή και ως μέθοδος regula falsi. Αυτή η μέθοδος χρησιμοποιείται για την εύρεση της ρίζας μιας συνάρτησης προσεγγίζοντάς την ως συντεταγμένη x όπου μια ευθεία γραμμή που συνδέει δύο σημεία στην καμπύλη συνάρτησης τέμνει τον άξονα x.
Μεθοδολογία:
- Αρχική εικασία: Επιλέξτε δύο αρχικά σημεία, x0 και x1, έτσι ώστε τα f(x0) και f(x1) να έχουν αντίθετα πρόσημα. Αυτά τα σημεία πρέπει να είναι κοντά στη ρίζα.
- Προβολή γραμμής: Υπολογίστε την εξίσωση της ευθείας που διέρχεται από τα σημεία (x0, f(x0)) και (x1, f(x1)). Η εξίσωση της γραμμής μπορεί να ληφθεί χρησιμοποιώντας τη μορφή κλίσης σημείου ή τη μορφή δύο σημείων.
- Τομή: Βρείτε τη συντεταγμένη x όπου η ευθεία τέμνει τον άξονα x λύνοντας την εξίσωση f(x) = 0. Αυτή η συντεταγμένη x είναι μια βελτιωμένη προσέγγιση της ρίζας.
- Ενημέρωση: Ενημερώστε τα σημεία (x0, f(x0)) και (x1, f(x1)) με βάση το πρόσημο της f(x) στο σημείο τομής. Αν η f(x) έχει το ίδιο πρόσημο με την f(x0), ορίστε x0 = x; διαφορετικά, ορίστε x1 = x.
- Σύγκλιση: Επαναλάβετε τα βήματα 2-4 μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας ή έως ότου επιτευχθεί ένας μέγιστος αριθμός επαναλήψεων.
Παράδειγμα:
Ας βρούμε τη ρίζα της συνάρτησης f(x) = x^3 – 2x – 5 χρησιμοποιώντας τη μέθοδο μεταβλητής συμβολοσειράς.
- Αρχική εικασία: Επιλέξτε δύο αρχικά σημεία, x0 = 2 και x1 = 3. Αυτά τα σημεία ικανοποιούν f(x0) = -1 και f(x1) = 10, υποδεικνύοντας μια αλλαγή πρόσημου.
- Γραμμική παρεμβολή: Η εξίσωση της ευθείας που διέρχεται από (x0, f(x0)) και (x1, f(x1)) προσδιορίζεται χρησιμοποιώντας τη μορφή δύο σημείων:
y = f(x0) + (x – x0) * (f(x1) – f(x0)) / (x1 – x0)
- Τομή: Λύστε την εξίσωση f(x) = 0 για να βρείτε τη συντεταγμένη x του σημείου τομής. Σε αυτήν την περίπτωση, λύνουμε x^3 – 2x – 5 = 0 για να λάβουμε x ≈ 2,5225225225225225.
- Ενημέρωση: Ενημερώστε τα σημεία x0 και x1 με βάση το πρόσημο της f(x) στο σημείο τομής. Εφόσον η f(x) έχει το ίδιο πρόσημο με τη f(x0), θέτουμε x0 = 2,5225225225225225.
- Σύγκλιση: Επαναλάβετε τα βήματα 2-4 μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας ή έως ότου επιτευχθεί ένας μέγιστος αριθμός επαναλήψεων.
Ακολουθεί μια περίληψη των επαναλήψεων:
- Επανάληψη 1: x0 = 2,5225225225225225, x1 = 3, Τομή ≈ 2,5225225225225225
- Επανάληψη 2: x0 = 2,5225225225225225, x1 = 2,9628871916817356, Τομή ≈ 2,9628871916817356
- Επανάληψη 3: x0 = 2,5225225225225225, x1 = 2,8108000747221343, Τομή ≈ 2,8108000747221343
- Επανάληψη 4: x0 = 2,5225225225225225, x1 = 2,695992017329196, Τομή ≈ 2,695992017329196
Μετά από μερικές επαναλήψεις, έχουμε μια βελτιωμένη προσέγγιση της ρίζας ως x ≈ 2,695992017329196. Μπορούμε να συνεχίσουμε τις επαναλήψεις μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας.
Η μέθοδος της μεταβαλλόμενης χορδής βελτιώνει επαναληπτικά την προσέγγιση της ρίζας κατασκευάζοντας μια γραμμή που συνδέει δύο σημεία στην καμπύλη συνάρτησης και βρίσκοντας την τομή της με τον άξονα x. Παρέχει μια ισχυρή προσέγγιση για την εύρεση των ριζών των συναρτήσεων, ειδικά όταν η συνάρτηση είναι μη γραμμική ή παρουσιάζει σύνθετη συμπεριφορά.
|
function |
output |
|
% Define the function f(x) f = @(x) x^3 +x -1 ;
% Set initial guesses and other parameters x0 = 0; x1 = 1; max_iterations = 2; tolerance = 1e-6;
% Call the variable_string_method function root = modified_regula_falsi(f, x0, x1, max_iterations, tolerance); disp(root); % Display the approximate root
function root = modified_regula_falsi(f, x0, x1, max_iterations, tolerance) % f: Function handle for the function f(x) % x0, x1: Initial guesses for the root % max_iterations: Maximum number of iterations % tolerance: Desired tolerance for the root approximation
% Initialize variables iteration = 0; error = inf;
% Perform variable string iterations while error > tolerance && iteration < max_iterations % Compute the intersection point with the x-axis x = x1 – f(x1) * (x1 – x0) / (f(x1) – f(x0));
% Calculate the error error = abs(x – x1);
% Check the sign of f(x) at the intersection point if f(x) * f(x0) > 0 x0 = x; else x1 = x; end
% Increment the iteration count iteration = iteration + 1; end
% Check convergence if iteration == max_iterations && error > tolerance disp(‘Variable string method did not converge within the specified number of iterations.’); root = NaN; % Return NaN for unsuccessful convergence else disp(‘Variable string method converged to the root:’); root = x; % Return the approximate root end end
|
Variable string method converged to the root: 2 |
Επιλυση γραμμικων συστηματων
Η επίλυση γραμμικών συστημάτων με αριθμητική ανάλυση είναι μια ισχυρή προσέγγιση που μας επιτρέπει να βρούμε κατά προσέγγιση λύσεις σε πολύπλοκα συστήματα γραμμικών εξισώσεων. Αυτή η μέθοδος περιλαμβάνει τη μετατροπή του αρχικού συστήματος σε αριθμητική μορφή και την εφαρμογή υπολογιστικών αλγορίθμων για την απόκτηση λύσεων. Χρησιμοποιώντας τεχνικές όπως η εξάλειψη Gauss, η αποσύνθεση LU ή επαναληπτικές μέθοδοι όπως ο Jacobi ή ο Gauss-Seidel, η αριθμητική ανάλυση μας παρέχει έναν πρακτικό και αποτελεσματικό τρόπο αντιμετώπισης συστημάτων με μεγάλους αριθμούς εξισώσεων και μεταβλητών. Διαδραματίζει ζωτικό ρόλο σε διάφορους τομείς, όπως η μηχανική, η φυσική, τα οικονομικά και η επιστήμη των υπολογιστών, όπου οι ακριβείς λύσεις σε γραμμικά συστήματα είναι απαραίτητες για τη μοντελοποίηση και την επίλυση προβλημάτων. Μέσω της αριθμητικής ανάλυσης, μπορούμε να ξεκλειδώσουμε τη δυνατότητα ανάλυσης περίπλοκων συστημάτων και τη λήψη τεκμηριωμένων αποφάσεων με βάση αξιόπιστες προσεγγίσεις.
Περιεχόμενα –
Επίλυση γραμμικών συστημάτων:
- Μέθοδος Κράμερ
- Μέθοδος Gauss
- Μέθοδος LU
- Μέθοδος Cholesky
- Μέθοδος Jacobi
- Μέθοδος Gauss-seidel
Μεθοδολογία:
- Ο κανόνας του Kramer είναι μια μέθοδος για την επίλυση ενός συστήματος γραμμικών εξισώσεων χρησιμοποιώντας ορίζουσες. Εφαρμόζεται σε τετραγωνικά συστήματα γραμμικών εξισώσεων, όπου ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των αγνώστων.
- Θεωρήστε ένα σύστημα γραμμικών εξισώσεων σε μορφή πίνακα: Ax = b, όπου A είναι ο πίνακας συντελεστών, x είναι το διάνυσμα των αγνώστων και b το διάνυσμα των σταθερών.
- Για να εφαρμόσουμε τον κανόνα του Kramer, υπολογίζουμε την ορίζουσα του πίνακα συντελεστών A, που συμβολίζεται ως det(A).
- Στη συνέχεια, υπολογίζουμε την ορίζουσα κάθε επαυξημένης μήτρας που προκύπτει αντικαθιστώντας μία στήλη του Α με το διάνυσμα b. Ας ονομάσουμε αυτές τις ορίζουσες det(Ai), όπου Ai είναι ο πίνακας που προκύπτει αντικαθιστώντας την i-η στήλη του A με b.
- Η λύση στο σύστημα των γραμμικών εξισώσεων δίνεται από το xi = det(Ai) / det(A), όπου xi είναι η τιμή του i-ου αγνώστου.
- Ο κανόνας του Kramer παρέχει έναν άμεσο τρόπο εύρεσης των τιμών των αγνώστων χωρίς ρητή επίλυση του συστήματος χρησιμοποιώντας μεθόδους όπως η Gaussian elimination.
Παράδειγμα:
Ας εξετάσουμε το ακόλουθο σύστημα γραμμικών εξισώσεων:
2x + 3y = 8
4x – 5y = -7
- Γράψτε το σύστημα των εξισώσεων σε μορφή πίνακα:
A = [[2, 3],
[4, -5]]
x = [x, y]
b = [8, -7]
- Υπολογίστε την ορίζουσα του πίνακα συντελεστών Α:
det(A) = 2*(-5) – 4*3 = -22
- Αντικαταστήστε την πρώτη στήλη του A με το διάνυσμα b για να λάβετε το A1:
A1 = [[8, 3],
[-7, -5]]
Υπολογίστε την ορίζουσα det(A1):
det(A1) = 8*(-5) – (-7)*3 = -26
- Αντικαταστήστε τη δεύτερη στήλη του A με το διάνυσμα b για να λάβετε το A2:
A2 = [[2, 8],
[4, -7]]
Υπολογίστε την ορίζουσα det(A2):
det(A2) = 2*(-7) – 4*8 = -46
- Υπολογίστε τους αγνώστους χρησιμοποιώντας τον κανόνα του Kramer:
x = det(A1) / det(A) = -26 / -22 = 1,1818
y = det(A2) / det(A) = -46 / -22 = 2,0909
Επομένως, η λύση στο σύστημα των γραμμικών εξισώσεων είναι x = 1,1818 και y = 2,0909.
Ο κανόνας του Kramer παρέχει μια εναλλακτική μέθοδο για την επίλυση γραμμικών συστημάτων, ιδιαίτερα χρήσιμη όταν ο αριθμός των αγνώστων είναι σχετικά μικρός. Ωστόσο, είναι υπολογιστικά ακριβό και λιγότερο αποδοτικό σε σύγκριση με άλλες μεθόδους για μεγαλύτερα συστήματα.
Σε αυτόν τον κώδικα, η συνάρτηση kramers_rule παίρνει ως είσοδο τον πίνακα συντελεστών A και το διάνυσμα των σταθερών b. Υπολογίζει την ορίζουσα του πίνακα συντελεστών det_A και στη συνέχεια εφαρμόζει τον κανόνα του Kramer για να βρει κάθε άγνωστο x(i).
Για να χρησιμοποιήσετε τον κώδικα, μπορείτε να ορίσετε τον δικό σας πίνακα συντελεστών A και το διάνυσμα των σταθερών b. Στη συνέχεια, καλέστε τη συνάρτηση kramers_rule με τα A και b ως ορίσματα και θα επιστρέψει το διάνυσμα λύσης x. Τέλος, μπορείτε να εμφανίσετε το διάνυσμα λύσης χρησιμοποιώντας το disp(x).
|
function |
output |
|
% Example usage: A = [2, 3; 4, -5]; % Coefficient matrix b = [8; -7]; % Vector of constants % Call the kramers_rule function to solve the linear system x = kramers_rule(A, b); disp(x); % Display the solution vector function x = kramers_rule(A, b) % A: Coefficient matrix of the linear system % b: Vector of constants n = size(A, 1); % Size of the system (number of unknowns) % Calculate the determinant of the coefficient matrix A det_A = det(A); x = zeros(n, 1); % Initialize the solution vector % Apply Kramer’s rule to find each unknown for i = 1:n Ai = A; % Create a copy of the coefficient matrix A Ai(:, i) = b; % Replace the i-th column with the vector b % Calculate the determinant of the modified matrix det_Ai = det(Ai); % Calculate the i-th unknown using Kramer’s rule x(i) = det_Ai / det_A; end end |
0.8636 2.0909 |
Μεθοδολογία:
- Η μέθοδος Gauss, γνωστή και ως Gaussian elimination, είναι ένας αλγόριθμος που χρησιμοποιείται για την επίλυση συστημάτων γραμμικών εξισώσεων μετατρέποντας τον επαυξημένο πίνακα σε μορφή γραμμής-βαθμίδας ή μειωμένη μορφή κλιμακίου σειράς.
- Δίνεται ένα σύστημα γραμμικών εξισώσεων σε μορφή πίνακα: Ax = b, όπου A είναι ο πίνακας συντελεστών, x είναι το διάνυσμα των αγνώστων και b το διάνυσμα των σταθερών.
- Η μέθοδος Gauss προχωρά εκτελώντας πράξεις στοιχειώδους σειράς στον επαυξημένο πίνακα [A | β] για την εξάλειψη των συντελεστών κάτω από την κύρια διαγώνιο.
- Οι πράξεις βασικής σειράς περιλαμβάνουν:
– Κλιμάκωση μιας γραμμής κατά μη μηδενική σταθερά.
– Ανταλλαγή δύο σειρών.
– Προσθήκη ή αφαίρεση πολλαπλασίου μιας σειράς από μια άλλη σειρά.
- Ο στόχος είναι να μετατραπεί ο επαυξημένος πίνακας σε μορφή σειράς-βαθμίδας, όπου οι συντελεστές κάτω από την κύρια διαγώνιο είναι όλοι μηδενικοί.
- Μόλις ληφθεί η μορφή γραμμής-βαθμίδας, εφαρμόζεται αντικατάσταση πίσω για να βρεθούν οι τιμές των αγνώστων.
- Η αντικατάσταση πίσω ξεκινά από την τελευταία σειρά και λύνει κάθε άγνωστο αντικαθιστώντας τις γνωστές τιμές από τις ήδη λυμένες σειρές.
- Εάν το σύστημα έχει μια μοναδική λύση, θα ληφθεί μετά την αλλαγή πλάτης. Εάν το σύστημα είναι ασυνεπές ή έχει άπειρες λύσεις, θα εντοπιστεί κατά τη διάρκεια της διαδικασίας.
Παράδειγμα:
Ας εξετάσουμε το ακόλουθο σύστημα γραμμικών εξισώσεων:
2x + 3y – z = 7
4x – 2y + 2z = 4
-2x + 2y + 4z = -2
ΛΥΣΗ
- Γράψτε το σύστημα εξισώσεων σε μορφή επαυξημένου μητρώου:
[2, 3, -1 | 7]
[4, -2, 2 | 4]
[-2, 2, 4 | -2]
- Εφαρμόστε τη μέθοδο Gauss για να μετατρέψετε τον επαυξημένο πίνακα σε μορφή σειράς-βαθμού:
[2, 3, -1 | 7] (R1)
[0, -8, 4 | -10] (R2′ = R2 – 2*R1)
[0, 0, 6 | 6] (R3′ = R3 + R1)
- Λαμβάνεται η φόρμα γραμμής-βαθμίδας και προχωράμε με αντικατάσταση πίσω για να βρούμε τις τιμές των αγνώστων:
6z = 6 => z = 1
-8y + 4z = -10 => -8y + 4 = -10 => -8y = -14 => y = 7/4
2x + 3y – z = 7 => 2x + 3(7/4) – 1 = 7 => 2x + 21/4 – 1 = 7 => 2x = 5/4 => x = 5/8
Επομένως, η λύση στο σύστημα των γραμμικών εξισώσεων είναι x = 5/8, y = 7/4, z = 1.
Η μέθοδος Gauss είναι ένας θεμελιώδης αλγόριθμος για την επίλυση γραμμικών συστημάτων και μπορεί να επεκταθεί για να χειριστεί μεγαλύτερα συστήματα. Παρέχει μια αποτελεσματική και αξιόπιστη προσέγγιση για την απόκτηση λύσεων σε γραμμικές εξισώσεις.
Σε αυτόν τον κώδικα, η συνάρτηση gauss_elimination παίρνει ως είσοδο τον πίνακα συντελεστών A και το διάνυσμα των σταθερών b. Εκτελεί τον αλγόριθμο εξάλειψης Gauss για να μετασχηματίσει τον επαυξημένο πίνακα [A | b] σε μορφή row-echelon και στη συνέχεια εφαρμόζει αντικατάσταση για να βρει τις τιμές των αγνώστων.
Για να χρησιμοποιήσετε τον κώδικα, μπορείτε να ορίσετε τον δικό σας πίνακα συντελεστών A και το διάνυσμα των σταθερών b. Στη συνέχεια, καλέστε τη συνάρτηση gauss_elimination με τα A και b ως ορίσματα, και θα επιστρέψει το διάνυσμα λύσης x. Τέλος, μπορείτε να εμφανίσετε το διάνυσμα λύσης χρησιμοποιώντας το disp(x).
Σημειώστε ότι ο κώδικας προϋποθέτει ότι ο πίνακας συντελεστών Α είναι αντιστρέψιμος και το σύστημα έχει μια μοναδική λύση.
|
function |
output |
|
% Example usage: A = [2, 3, -1; 4, -2, 2; -2, 2, 4]; % Coefficient matrix b = [7; 4; -2]; % Vector of constants % Call the gauss_elimination function to solve the linear system x = gauss_elimination(A, b); disp(x); % Display the solution vector function x = gauss_elimination(A, b) % A: Coefficient matrix of the linear system % b: Vector of constants n = size(A, 1); % Size of the system (number of unknowns) % Augmented matrix [A | b] aug_mat = [A, b]; % Forward elimination to transform to row-echelon form for k = 1:n-1 for i = k+1:n factor = aug_mat(i, k) / aug_mat(k, k); aug_mat(i, 🙂 = aug_mat(i, 🙂 – factor * aug_mat(k, :); end end % Back substitution to find the unknowns x = zeros(n, 1); x(n) = aug_mat(n, n+1) / aug_mat(n, n); for i = n-1:-1:1 x(i) = (aug_mat(i, n+1) – aug_mat(i, i+1:n) * x(i+1:n)) / aug_mat(i, i); end end |
1.6818 1.1364 -0.2273 |
Η μέθοδος αποσύνθεσης LU βασίζεται στην αποσύνθεση του πίνακα συντελεστών ενός γραμμικού συστήματος στο γινόμενο ενός κατώτερου τριγωνικού πίνακα (L) και ενός ανώτερου τριγωνικού πίνακα (U). Αυτή η αποσύνθεση μας επιτρέπει να λύσουμε το σύστημα πιο αποτελεσματικά.
Ακολουθεί η μεθοδολογία για τη μέθοδο αποσύνθεσης LU:
- Δίνεται ένα γραμμικό σύστημα εξισώσεων με τον πίνακα συντελεστών Α και το διάνυσμα των σταθερών β.
- Πραγματοποιήστε αποσύνθεση LU του πίνακα συντελεστών A, έτσι ώστε A = LU, όπου L είναι ο κάτω τριγωνικός πίνακας και U είναι ο ανώτερος τριγωνικός πίνακας.
- Λύστε το σύστημα Lc = b για το c με μπροστινή αντικατάσταση, όπου c είναι ένα προσωρινό διάνυσμα.
- Λύστε το σύστημα Ux = c για x με αντίστροφη αντικατάσταση, όπου x είναι το διάνυσμα της λύσης.
Η μέθοδος αποσύνθεσης LU παρέχει μια παραγοντοποίηση του πίνακα συντελεστών Α, ο οποίος μπορεί να επαναχρησιμοποιηθεί για την επίλυση πολλαπλών γραμμικών συστημάτων με τον ίδιο πίνακα συντελεστών αλλά με διαφορετικά σταθερά διανύσματα αποτελεσματικά.
Παράδειγμα:
Εξετάστε το ακόλουθο γραμμικό σύστημα:
2x + 3y – z = 7
4x – 2y + 2z = 4
-2x + 2y + 4z = -2
ΛΥΣΗ
Μπορούμε να γράψουμε αυτό το σύστημα σε μορφή πίνακα ως Ax = b, όπου:
A = [[2, 3, -1],
[4, -2, 2],
[-2, 2, 4]]
x = [[x],
[y],
[z]]
b = [[7],
[4],
[-2]]
Για να λύσουμε αυτό το σύστημα χρησιμοποιώντας τη μέθοδο αποσύνθεσης LU, εκτελούμε τα ακόλουθα βήματα:
- Εκτελέστε αποσύνθεση LU: A = LU. Ας υποθέσουμε ότι η αποσύνθεση μας δίνει:
L = [[1, 0, 0],
[2, 1, 0],
[-1, 3, 1]]
U = [[2, 3, -1],
[0, -8, 4],
[0, 0, 2]]
- Λύστε το σύστημα Lc = b για το c με μπροστινή αντικατάσταση:
c = [[c1],
[c2],
[c3]]
Χρησιμοποιώντας την αντικατάσταση προς τα εμπρός, μπορούμε να βρούμε τις τιμές του c:
c1 = b1 = 7
c2 = b2 – 2 * c1 = 4 – 2 * 7 = -10
c3 = b3 – (-1) * c1 – 3 * c2 = -2 – (-1) * 7 – 3 * (-10) = 22
- Λύστε το σύστημα Ux = c για x με αντικατάσταση προς τα πίσω:
x = [[x],
[y],
[z]]
Χρησιμοποιώντας την αντικατάσταση πίσω, μπορούμε να βρούμε τις τιμές του x:
z = c3 / U33 = 22 / 2 = 11
y = (c2 – U23 * z) / U22 = (-10 – 4 * 11) / -8 = -3
x = (c1 – U12 * y – U13 * z) / U11 = (7 – 3 * (-3) – (-1) * 11) / 2 = 1
Επομένως, η λύση στο γραμμικό σύστημα είναι x = 1, y = -3, z = 11.
Αυτή είναι η βασική μεθοδολογία της μεθόδου αποσύνθεσης LU για την επίλυση γραμμικών συστημάτων. Αποσυνθέτοντας τον πίνακα συντελεστών σε κάτω και άνω τριγωνικούς πίνακες, μπορούμε να λύσουμε αποτελεσματικά το σύστημα χρησιμοποιώντας το μπροστινό.
Η μέθοδος Cholesky είναι μια εξειδικευμένη τεχνική που χρησιμοποιείται για την επίλυση συμμετρικών και θετικών ορισμένων γραμμικών συστημάτων εξισώσεων. Βασίζεται στην αποσύνθεση του Cholesky, η οποία επηρεάζει τον συντελεστή μήτρας Α στο γινόμενο ενός κατώτερου τριγωνικού πίνακα L και στη μετατόπισή του L^T.
ΜΕΘΟΔΟΛΟΓΙΑ
Τα βήματα που περιλαμβάνονται στη μέθοδο Cholesky είναι τα εξής:
- Ελέγξτε εάν ο πίνακας συντελεστών Α είναι συμμετρικός και θετικός ορισμένος. Εάν δεν είναι, η μέθοδος δεν μπορεί να εφαρμοστεί.
- Υπολογίστε την αποσύνθεση Cholesky του A ως L * L^T, όπου L είναι ένας χαμηλότερος τριγωνικός πίνακας. Αυτή η αποσύνθεση μπορεί να επιτευχθεί χρησιμοποιώντας τον αλγόριθμο παραγοντοποίησης Cholesky.
- Λύστε το σύστημα L * y = b για το y, όπου L είναι ο κατώτερος τριγωνικός πίνακας που προκύπτει από την αποσύνθεση του Cholesky και b είναι το διάνυσμα των σταθερών.
- Λύστε το σύστημα L^T * x = y για x, όπου L^T είναι η μετάθεση του κάτω τριγωνικού πίνακα L και y είναι η λύση που λήφθηκε στο προηγούμενο βήμα.
- Η λύση στο αρχικό γραμμικό σύστημα είναι το διάνυσμα x που λήφθηκε στο προηγούμενο βήμα.
Η μέθοδος Cholesky είναι υπολογιστικά αποδοτική και αριθμητικά σταθερή για συμμετρικά και θετικά καθορισμένα συστήματα. Μειώνει την υπολογιστική πολυπλοκότητα σε σύγκριση με άλλες μεθόδους όπως η Gaussian elimination.
Η μέθοδος Jacobi είναι ένας επαναληπτικός αλγόριθμος που χρησιμοποιείται για την επίλυση γραμμικών συστημάτων εξισώσεων. Ανήκει στην κατηγορία των στατικών επαναληπτικών μεθόδων, όπου η λύση λαμβάνεται με επαναληπτική ενημέρωση μιας αρχικής προσέγγισης μέχρι να επιτευχθεί σύγκλιση.
ΜΕΘΟΔΟΛΟΓΙΑ
Τα βήματα που περιλαμβάνονται στη μέθοδο Jacobi είναι τα εξής:
- Με δεδομένο ένα γραμμικό σύστημα Ax = b, αποσυνθέστε τον πίνακα συντελεστών A στο άθροισμα των διαγωνίων (D), του κατώτερου τριγωνικού (L) και του άνω τριγωνικού (U), έτσι ώστε A = D + L + U. Εδώ, το D περιέχει τα διαγώνια στοιχεία του A, L περιέχει τα κάτω τριγωνικά στοιχεία και το U περιέχει τα ανώτερα τριγωνικά στοιχεία.
- Αναδιάταξη του γραμμικού συστήματος ως x = D^(-1) * (b – (L + U) * x), όπου D^(-1) είναι το αντίστροφο του διαγώνιου πίνακα D. Αυτή η εξίσωση αντιπροσωπεύει τον τύπο επανάληψης για ενημέρωση το διάνυσμα λύσης x.
- Αρχικοποιήστε μια αρχική εικασία για το διάνυσμα λύσης x.
- Επαναλάβετε χρησιμοποιώντας τον τύπο επανάληψης Jacobi μέχρι να επιτευχθεί σύγκλιση. Σε κάθε επανάληψη, ενημερώστε το διάνυσμα λύσης x χρησιμοποιώντας τον τύπο επανάληψης που ελήφθη στο βήμα 2.
- Επαναλάβετε το βήμα 4 μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας ή να ξεπεραστεί ο μέγιστος αριθμός επαναλήψεων.
- Η τελική λύση είναι το διάνυσμα συγκλίνουσας λύσης x.
Η μέθοδος Jacobi μπορεί να συγκλίνει αργά για ορισμένα γραμμικά συστήματα ή μπορεί να αποτύχει να συγκλίνει για άλλα. Λειτουργεί καλύτερα για διαγώνια κυρίαρχα ή συμμετρικά θετικά καθορισμένα συστήματα.
Η μέθοδος Gauss-Seidel είναι ένας επαναληπτικός αλγόριθμος που χρησιμοποιείται για την επίλυση γραμμικών συστημάτων εξισώσεων. Ανήκει στην κατηγορία των στατικών επαναληπτικών μεθόδων, όπου η λύση λαμβάνεται με επαναληπτική ενημέρωση μιας αρχικής προσέγγισης μέχρι να επιτευχθεί σύγκλιση.
ΜΕΘΟΔΟΛΟΓΙΑ
Τα βήματα που περιλαμβάνονται στη μέθοδο Gauss-Seidel είναι τα εξής:
- Δεδομένου ενός γραμμικού συστήματος Ax = b, αποσυνθέστε τον πίνακα συντελεστών A στο άθροισμα των διαγωνίων (D), του κατώτερου τριγωνικού (L) και του άνω τριγωνικού (U), έτσι ώστε A = D + L + U. Εδώ, το D περιέχει τα διαγώνια στοιχεία του A, L περιέχουν τα αυστηρά κάτω τριγωνικά στοιχεία και το U περιέχει τα αυστηρά ανώτερα τριγωνικά στοιχεία.
- Αναδιάταξη του γραμμικού συστήματος ως (D + L)x = b – Ux. Αυτή η εξίσωση αντιπροσωπεύει τον τύπο επανάληψης για την ενημέρωση του διανύσματος λύσης x.
- Αρχικοποιήστε μια αρχική εικασία για το διάνυσμα λύσης x.
- Επαναλάβετε χρησιμοποιώντας τον τύπο επανάληψης Gauss-Seidel μέχρι να επιτευχθεί σύγκλιση. Σε κάθε επανάληψη, ενημερώστε κάθε στοιχείο του διανύσματος λύσης x χρησιμοποιώντας τις τρέχουσες και τις ενημερωμένες τιμές των άλλων συστατικών.
- Επαναλάβετε το βήμα 4 μέχρι να επιτευχθεί το επιθυμητό επίπεδο ακρίβειας ή να ξεπεραστεί ο μέγιστος αριθμός επαναλήψεων.
- Η τελική λύση είναι το διάνυσμα συγκλίνουσας λύσης x.
Η μέθοδος Gauss-Seidel συγκλίνει γενικά ταχύτερα από τη μέθοδο Jacobi για τα περισσότερα γραμμικά συστήματα. Λειτουργεί καλύτερα για διαγώνια κυρίαρχα ή συμμετρικά θετικά καθορισμένα συστήματα.
ΙΔΙΟΤΙΜΕΣ - ΙΔΙΟΔΙΑΝΥΣΜΑΤΑ
Μέθοδος δυνάμεων
Η μέθοδος των δυνάμεων είναι ένας επαναληπτικός αλγόριθμος που χρησιμοποιείται για να προσεγγίσει την μεγαλύτερη σε μέγεθος κατά απόλυτη τιμή ιδιοτιμή και το ιδιοδιάνυσμα ενός τετραγωνικού πίνακα. Η μέθοδος βασίζεται στο γεγονός ότι εάν ξεκινήσουμε με ένα αρχικό διάνυσμα και το πολλαπλασιάσουμε επανειλημμένα με τον πίνακα, το διάνυσμα που προκύπτει θα συγκλίνει στο μεγαλύτερο σε μέγεθος κατ απόλυτη τιμή ιδιοδιάνυσμα καθώς αυξάνεται ο αριθμός των επαναλήψεων.
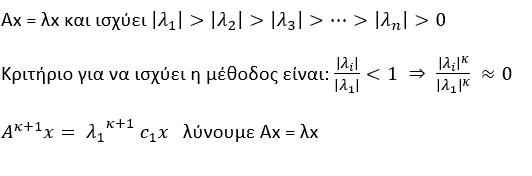
Ακολουθεί η μεθοδολογία βήμα προς βήμα της μεθόδου των δυνάμεων:
- Επιλέγουμε ένα αρχικό μη μηδενικό διάνυσμα x(0) κατάλληλων διαστάσεων.
- Για κάθε επανάληψη k = 1, 2, …, μέχρι τη σύγκλιση:
- Υπολογίζουμε το γινόμενο y(k) = A * x(k-1), όπου A είναι ο δεδομένος πίνακας.
- Κανονικοποιούμε το διάνυσμα που προκύπτει διαιρώντας με το μεγαλύτερο στοιχείο του: x(k) = y(k) / max(|y(k)|).
- Υπολογίζουμε την προσέγγιση της ιδιοτιμής: λ(k) = (x(k))’ * A * x(k), όπου το (x(k))’ υποδηλώνει τη μετάθεση του x(k).
- Ελέγχουμε για κριτήρια σύγκλισης, όπως η διαφορά στην προσέγγιση της ιδιοτιμής μεταξύ των επαναλήψεων ή ο κανόνας της διαφοράς μεταξύ x(k) και x(k-1).
- Εάν πληρούνται τα κριτήρια σύγκλισης, τερματίζουμε τις επαναλήψεις και εξάγουμετην προσέγγιση της ιδιοτιμής λ(k) και το αντίστοιχο ιδιοδιάνυσμα x(k).
Περιεχόμενα –
Ιδιοτιμές – Ιδιοδιανύσματα:


Συνέχεια στο Matlab
Παράδειγμα 1:
Να βρεθεί η μεγαλύτερη σε μέγεθος ιδιοτιμή και το ιδιοδιάνυσμα του ακόλουθου πίνακα:

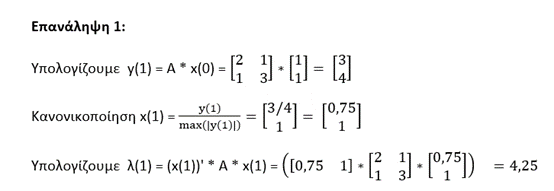
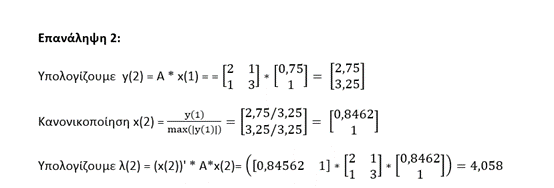
Η διαδικασία συνεχίζεται μέχρι να εκπληρωθούν τα κριτήρια σύγκλισης.
Παράδειγμα 2:
Ας βρούμε την μεγαλύτερη ιδιοτιμή και το ιδιοδιάνυσμα του ακόλουθου πίνακα:
Α = [0,8, 0,3; 0,2, 0,7]
- Βήμα 1: Επιλέξτε ένα αρχικό διάνυσμα x(0). Ας πάρουμε x(0) = [1; 1].
- Επανάληψη 1:
Υπολογίστε y(1) = A * x(0) = [0,8, 0,3; 0.2, 0,7] * [1; 1] = [1,1; 0,9]
Κανονικοποίηση x(1) = y(1) / max(|y(1)|) = [1,1/1,1; 0,9/1,1] = [1; 0,8182]
Υπολογίστε λ(1) = (x(1))’ * A * x(1) = ([1; 0,8182])’ * [0,8, 0,3; 0,2, 0,7] * [1; 0,8182] = 1,545
- Επανάληψη 2:
Υπολογίστε y(2) = A * x(1) = [0,8, 0,3; 0,2, 0,7] * [1; 0,8182] = [1,0364; 0,8182]
Κανονικοποίηση x(2) = y(2) / max(|y(2)|) = [1,0364/1,0364; 0,8182/1,0364] = [1; 0,7895]
Υπολογίστε λ(2) = (x(2))’ * A * x(2) = ([1; 0,7895])’ * [0,8, 0,3; 0,2, 0,7] * [1; 0,7895] = 1,493
Και πάλι, η διαδικασία συνεχίζεται μέχρι να εκπληρωθούν τα κριτήρια σύγκλισης.
Είναι σημαντικό να σημειωθεί ότι η μέθοδος των δυνάμεων μπορεί να μην συγκλίνει εάν ο πίνακας έχει πολλαπλές ιδιοτιμές με παρόμοια μεγέθη ή εάν το αρχικό διάνυσμα δεν έχει επιλεγεί σωστά. Επιπλέον, η μέθοδος είναι κατά κύριο λόγο κατάλληλη για την εύρεση της κυρίαρχης ιδιοτιμής και του ιδιοδιανύσματος ενός πίνακα.
Μέθοδος εκτροπής
H μέθοδος εκτροπής υπολογίζει όλες τις ιδιοτιμές και τα ιδιοδιανύσματα ενός τετραγωνικού πίνακα A.

Μετατοπισμένη μέθοδος των δυνάμεων
Όταν δεν συγκλίνει η μέθοδος των δυνάμεων
(Α – mI)x = Ax – mIx = λx – mIx = x( λ – mI )
Η μετατοπισμένη μέθοδος των δυνάμεων βρίσκει ακριβώς τα ίδια ιδιοδιανύσματα άλλα είδη τιμές τους είναι οι λi και λi-m
Αντίστροφη μέθοδος των δυνάμεων
Η αντίστροφη μέθοδος των δυνάμεων είναι ένας επαναληπτικός αλγόριθμος που χρησιμοποιείται για να προσεγγίσει την μικρότερη σε μέγεθος κατά απόλυτη τιμή ιδιοτιμή και το ιδιοδιάνυσμα ενός τετραγωνικού πίνακα.
Το Α και το Α^(-1) έχουν τα ίδια ιδιοδιανύσματα και αν λi είναι οι ιδιοτιμές του Α τότε το Α^(-1) έχει για ιδιοτιμές τις 1/ λi.
Αν λn είναι η μικρότερη ιδιοτιμή του Α τότε η 1/λn είναι η μεγαλύτερη ιδιοτιμή του Α^(-1).
Οπότε αν εφαρμόσουμε την μέθοδο των δυνάμεων στο Α^(-1) θα βρούμε την ιδιοτιμή 1/λn όπου η λn θα είναι η μικρότερη ιδιοτιμή του Α.
Μέθοδος QR
Η μέθοδος QR είναι ένας επαναληπτικός αλγόριθμος που χρησιμοποιείται για τον υπολογισμό των ιδιοτιμών και των ιδιοδιανυσμάτων ενός τετραγωνικού πίνακα Α πραγματοποιώντας το α σε 2 μητρώα Q και R
Όπου Q ένα μητρώο που έχει στήλες μια σειρά ορθογώνιων διανυσμάτων και R ένα μητρώο άνω τριγωνικό. Αποσυνθέτει μια δεδομένο μητρώο στο γινόμενο ενός ορθογώνιου πίνακα (Q) και ενός ανώτερου τριγωνικού πίνακα (R), ο οποίος επιτρέπει την εξαγωγή ιδιοτιμών μέσω επανάληψης.
Ακολουθεί μια μεθοδολογία βήμα προς βήμα για τη μέθοδο QR:



Βήμα 4ο : Σε αυτό το βήμα έχουμε βρει το μητρώο ( και πρέπει να ελέγξουμε αν ισχύει η σχέση
Βήμα 5ο : Επαναλαμβάνουμε αυτή την διαδικασία στο μητρώο Α1 (Α1 =RQ) που βρήκαμε στο βήμα 4 για να υπολογίσουμε το νέο μητρώο Α2 (Α2 =R1Q1) . Μετά από n επαναλήψεις το πλησιάζει σε τριγωνική μορφή οπότε οι ιδιοτιμές του είναι τα στοιχεία της διαγωνίου.
Μέθοδος QR με παράδειγμα:
Παράδειγμα 1:



Βήμα 4: Ελέγχουμε αν QR = A. Εάν ισχύει η ισότητα, προχωράμε στο επόμενο βήμα. Διαφορετικά, επιστρέφουμε στο Βήμα 2 και επαναλαμβάνουμε τη διαδικασία.
Βήμα 5: επαναλαμβάνουμε τη διαδικασία στον πίνακα Α1 = RQ που ελήφθη από το προηγούμενο βήμα για τον υπολογισμό του νέου πίνακα A2 ( A2 =R1Q1) . Επαναλαμβάνουμε αυτή τη διαδικασία μέχρι το An να πλησιάσει την τριγωνική μορφή, όπου οι ιδιοτιμές είναι τα στοιχεία στη διαγώνιο.
Σημείωση: Οι πραγματικοί υπολογισμοί μπορεί να περιλαμβάνουν περισσότερα δεκαδικά ψηφία, αλλά έχουμε στρογγυλοποιήσει τους αριθμούς για απλότητα σε αυτό το παράδειγμα.

